Chapter1 信息可视化 Visualizing Information
直方图(Histogram) 不同于条形图(Bar Chart),长方形之间不能有间隙,一是因为需要覆盖所有数值,二是区间宽度可以反映所覆盖数值范围的大小。
直方图的长方形面积代表每组的频率,长方形的高度用于度量一个特定组的频率的集中程度。
\(\begin{align} 频率密度 &= 频率/ 组距 \\ Frequency Density &= Frequency / Class Width \end{align}\)
如果组距足够小,我们就可以将图形看成一条曲线, 这条曲线就是概率论中的密度函数。
累积频率即到某个特定数值为止的总频率,即频率的累计总和 (running total)
将每组数据的上限和对应的累积频率描点连线就得到累积频率图。
Chapter2 集中趋势的量度 Measuring Central Tendency
平均数(average) 不止一种:均值、中位数、众数。
异常值(outliers) 的存在会抬高(拉低)均值,使数据偏斜 (skewed )
如果升序排列所有数据,outliers位于右边,则称数据向右偏斜 (skewed to the right )
向右偏斜的数据有一条“ 尾巴” ,这条尾巴由偏大异常值(high outliers)形成 , 向右逐渐变弱 (trail off)
偏大异常值抬高了均值,将均值拉向了右边,使得均值大于大部分值,失去了代表性。
理想情况下数据呈对称形态,均值位于中央, 均值不会被异常值拉向任何一侧,中央位置两侧的数据形状大致相同。
当异常值和偏斜数据使均值产生误导时, 我们可以对数据进行排序并取中间值,这个中间值是另一种平均数,称为中位数。求中位数三步法:
1)将数据从小到大排序
2)如果有奇数个数值,则中位数是位于正中间的那个数。如果有n个数,则中间数的位置为$(n+1)/2$
3)如果有偶数个数值,则将中间两个数相加然后除以2 。中间位置的算法也是 $(n+1)/2$ , 两个中间数分别位于这个中间位置的两侧。
中位数永远位于中间,受异常值影响小,稳健性比均值更好。对于均值,只要有一个异常值离得很远,均值就会变得很大。如果数据向右偏斜,则均值 $>$ 中位数,如果数据向左偏斜,则均值$<$中位数。
中位数一定比均值更优吗? 反例:
1)杂志社承诺处理稿件时间的中位数是7天,然而半个月过去了却音讯全无。因为中位数是7天意味着有50%可能性要花7天以上,7天以上是多久,这样的信息是中位数没有体现出来的。因此哪怕我们的文章被杂志社拖了一年,只要有另一篇文章在7天以内完成了处理,杂志社就达成了中位数7天的承诺。如果杂志社承诺的是处理稿件时间的均值为7天,那么如果我们的文章花了15天才处理完成,就要有另外2篇文章平均每篇只能花3天时间处理,或者另外4篇文章平均每篇只有5天时间,这样才能达成均值为7天的承诺。这无疑给杂志社施加了更大的压力,为了减轻压力,他们就不太可能用超过15天的时间来处理我们的文章。因此对我来说,我可以放心自己的文章不太可能被杂志社拖到两倍于均值以上的时间。
2)均值的计算比中位数更方便。计算中位数需要先排序,排序算法的时间复杂度比求算术平均更大。均值具有可加性,为了统计全国的平均收入,我们可以分别统计每个省的平均收入和人口数量,然后对所有省的平均收入做一个加权平均就可以得到全国人民的平均收入了。而如果统计的是每个省的人口数量和收入中位数,我们对全国人民的收入中位数还是一无所知。
总结:尽管均值、中位数都是统计学上的客观事实,哪一个更具有代表性却是一个主观的评价。在统计收入时,我们认为我们被马云“平均”了是一件坏事,因为马云是少数群体,是异常值,因此大部分人的收入都远远低于被马云平均之后的均值,因此认为均值不具有代表性,中位数才是群众的代表。然而在上面杂志社的例子中,我自己成为了异常值,因此我会认为中位数没有代表我这个样本,将异常值包含在内的平均数对我而言才具有代表性。当我不是马云的时候,我希望采用中位数,因为中位数更代表我;而当我变成马云的时候,中位数对我而言就失去了代表性,均值才有意义。
在分布差异过大的情况下,任何单一的统计量都不能描述整体分布。抛开分布曲线而选择单一描述符本身就是错误的。如果社会上三分之一的人收入都是一个亿,三分之二的收入只有一千块,中位数$1000$显然不能很好地描述这个社会的整体收入情况。
除了均值和中位数,还有第三种平均数,称为众数 (mode)。众数是一批数字中最常见的数值,即频数最大的数值。 与均值和中位数不同,众数必须是数据集中的一个数值,而且是最频繁出现的数值。
数据的众数可以不止一 个。如果有一个以上的数值具有最大频数,则每一个这样的数值都是众数。如果数据看上去体现了多种趋势或多批数据,那么我们就为每一批数据给出一个众数。如果一个数据集有两个众数,则我们说数据是双峰 (bimodal) 的。
Chapter3 分散性与变异性的量度 Measuring Variability and Spread
平均数只能确定一组数据的中心,却无法给出数据变动情况的信息。通过计算 Range (极差,也称全距), 我们可以初步获知数据的分散情况。全距 (极差) 描述了数据扩展的范围,就像在测量数据的宽度,计算方法是最大值减去最小值 (上界减下界)。
全距仅仅描述了数据的宽度,无法反映数据在上下界之间的真实分布,受异常值影响很大。为了消除异常值的影响,可以采用更小的距来度量,即找出全距中不包含异常值的部分。一种常用的迷你距 (Mini Range) 是四分位距 (IQR, InterQuartile Range ). 四分位距仅考虑数据中心(中位数) 附近的数值。构建四分位距的方法是先讲数据升序排列,然后将数据一分为四,每个数据块包含四分之一(25%) 的数据。
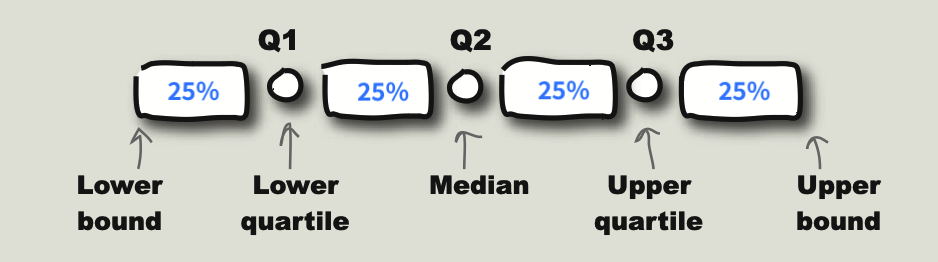
起到将整组数据一分为四作用的几个数被称为四分位数 (Quartile). 最小的四分位数$Q1$ 称为下四分位数(lower quartile) 或第1四分位数,最大的四分位数$Q3$称为上四位分数(upper quartile). 中间的四位分数$Q2$就是中位数. 四分位距的计算方法:$IQR = Q3 - Q1$. 第$k$ 个四分位数的计算方法:先看$\dfrac{k}{4}\cdot n$ 是不是整数,如果是整数,四分位数的位置在第$\dfrac{kn}{4}$ 和第$\dfrac{kn}{4}+1$ 个数之间,取则两个数的均值就得到第$k$个四分位数;如果不是整数则向上取整,第$\left\lceil \dfrac{kn}{4}\right\rceil$ 个数就是第$k$个四分位数.
四分位距 (IQR)不是构建mini range的唯一方法,如果将数据一分为十,每一个数据块包含$10\%$ 的数据,则起分割作用的数称为十分位数(deciles)。 十分位距 (IDR) 也很常用,计算方法是第9个十分位数和第1个十分位数之差,只考虑中间$80\%$ 的数据。如果将一组数据按百分比进行分割,则起分割作用的数称为百分位数 (percentiles)。第$k$ 个百分位数就是位于数据范围$k\%$处的数, 记为$P_k$. 四分位数其实也是一种百分位数,上四分位数即$P_{25}$ , 下四分位数即$P_{75}$. 百分位距 (IPR) 是指给定两个百分位数之差。尽管百分位距不常用,百分位数却对划分名次、排行很有用。假如你在测验中得了50分,仅看分数本身无法得知与其他人相比是好是坏。如果告诉你这次测验的第90个百分数是50分,即$P_{90}=50$, 就能知道你的分数高于或等于$90\%$ 的人. 百分位数的计算方法和四分位数相似,关键在于确定$\dfrac{kn}{100}$ 是否为整数。
箱线图(箱形图,box plot) 可以用来直观比较不同数据集的距。“箱”能显示四分位数和四分位数的位置,“线”能显示全距和上下界。
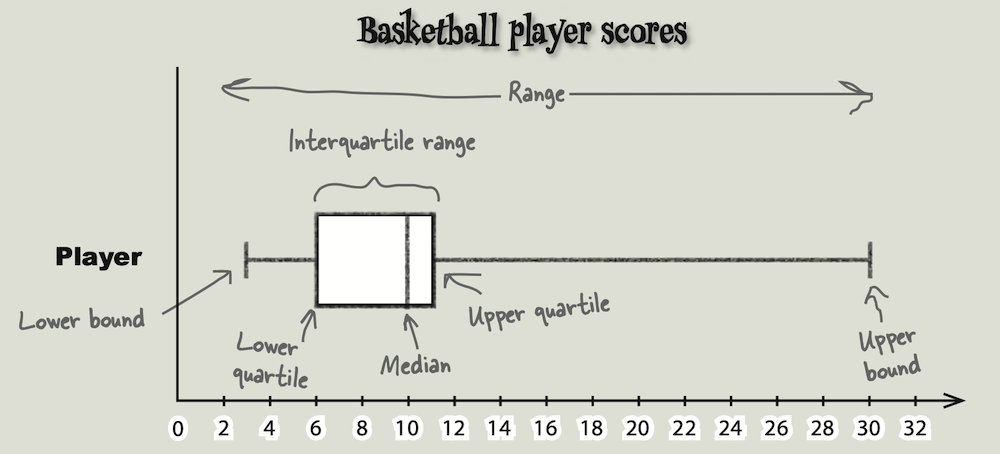
全距只计算了极值之差,受异常值影响很大,是一种对数据离散程度 (dispersion) 的粗略估计。四分位距仅仅考虑中间一部分数据,也不能全面地反映数据的分散性。在实际应用中,例如评估一名球员得分的稳定程度,我们需要知道接近数据中心的那些数值出现的频率。为了更精确地度量数据的变异性,我们可以观察每个数值与均值的距离。

考虑计算每个数值与均值 $\mu$ 的平均距离。例如有三个数值$1, 4, 9$, 均值$\mu=4$时
\(平均距离 = \dfrac{(1-4)+(2-4)+(9-4)}{3} = \dfrac{(-3)+(-2)+5}{3} = 0\) 我们发现如果把直接每个数值与均值相减,得到的正负距离会互相抵消,
因为这些距离之和 $\sum\limits_{i=1}^n (x_i - \mu) = \sum\limits_{i=1}^n x_i -\sum\limits_{i=1}^n\mu = 0 $ 那么平均距离永远是0,我们无法得到一个有用的统计量。
