等价关系与等价类的直观解释
等价关系就像是一个“相似性”的规则,用来判断两个东西是不是“差不多”。如果两个东西满足这个规则,我们就说它们是“等价”的。而等价类就是把所有“差不多”的东西放在一起,组成的一个小组。
等价关系与等价类是一种“分类”和“分组”的思想方法。日常生活中的例子:如果两个水果是同一种类,我们就说它们是“等价”的。比如,所有苹果都是等价的,所有香蕉都是等价的。把所有苹果放在一起,就是一个等价类$[苹果]$;把所有香蕉放在一起,就是另一个等价类$[香蕉]$。所有的水果被分成一个个等价类,这样我们就可以很方便地找到自己想吃的水果。计算机系统的例子:如果两个文件的类型相同,我们就说它们是“等价”的。把所有图片文件(如.jpg)放在一起,就是一个等价类;把所有文档文件(如.docx)放在一起,就是另一个等价类。这样,计算机就可以很方便地找到用户需要的文件。用户分组的例子:如果两个用户属于同一个兴趣小组,我们就说他们是等价的。比如,所有喜欢篮球的用户都是等价的,组成一个等价类$[篮球]$,所有喜欢足球的用户组成另一个等价类$[足球]$, 推荐系统就可以根据用户的兴趣给每个组推送合适的内容。
等价关系的定义
二元关系的定义 给定集合$A$ ,$A$上的一个二元关系 (binary relation) 是笛卡尔积$A\times A$ 的一个子集$\mathscr{R} \subseteq A\times A$ ,其中的有序对$(a,b)$ 存在某种关系。通常我们写作$a\ \mathscr{R}\ b$ 而不是$(a,b) \in \mathscr{R}$ .
二元关系举例 集合$A := \lbrace 1,2,3 \rbrace$.
考虑’$<$’ 关系,对应的有序对集合是$\bigl\lbrace{(1,2),(1,3),(2,3)\bigr\rbrace}$ . 因为$(1,2)$ 在关系所对应的有序对集合中,所以$1\lt 2$ 成立. 但$3\lt 1$不成立因为$(3,1)$ 不在集合中.
类似地,’$=$’ 关系定义为有序对的集合$\lbrace (1,1),(2,2),(3,3)\rbrace$
$A\times A$ 的任意子集都是一个关系. 例如我们可以通过$\lbrace(1,2),(2,1),(2,3),(3,1) \rbrace$ 定义一个关系$\dagger$ , 则$1\dagger 2$ 和 $3\dagger 1$ 都成立,但$1\dagger 3$ 不成立.
关系的基本性质 设$\mathscr{R}$是$A$上的二元关系. 我们称$\mathscr{R}$ 是
$(i)$ 自反的 (Reflexive) 如果对所有$a\in A$ 都有$a\ \mathscr{R} \ a$ .
$(ii)$ 对称的 (Symmetric) 如果 $a\ \mathscr{R}\ b \implies b\ \mathscr{R}\ a$ .
$(iii)$ 传递的 (Transitive) 如果 $a\ \mathscr{R}\ b$ 且 $b\ \mathscr{R}\ c \implies a\ \mathscr{R}\ c$ .
如果$\mathscr{R}$是自反、对称、传递的,我们称$\mathscr{R}$是一个等价关系 (equivalence relation) .
关系的性质举例 令$A:=\lbrace 1,2,3 \rbrace$ . $A$上的’$<$’ 关系是传递的,但既不是自反的也不是对称的. 定义为$\lbrace (1,1),(1,2),(1,3),(2,2),(2,3),(3,3)\rbrace$ 的’$\le$’ 关系是自反的和传递的,但不是对称的.
最后一个例子:定义一个关系$\star$ 为$\lbrace(1,1),(1,2),(2,1),(2,2),(3,3) \rbrace$. 这个关系是一个等价关系.
等价关系的作用在于它把一个集合划分成一个个由“等价的”(equivalent)元素组成的集合。
等价关系的典型例子:’模$m$同余’关系把$\mathbb{Z}$划分为$m$个等价类.
等价类的定义
令 $\mathscr{R}$ 是集合$A$上的一个等价关系. 元素 $a\in A$ 的一个等价类是集合$\lbrace x\in A \mid a \ \mathscr{R}\ x \rbrace$ , 记为$[a]$.
集合A在等价关系R下的等价类将集合A分解成了若干个不相交的子集
等价类的性质
令$\mathscr{R}$是$A$上的一个等价关系.
分解性 集合A在等价关系$\mathscr{R}$下的所有等价类组成集合$A$的一个划分.
(等价关系将$A$分解成互不相交的若干子集,所有等价类的并集是$A$本身且两个不同的等价类交集为空)
Proof. 先证覆盖性:对集合中任意元素$x \in A$, 根据等价关系的自反性有$x\ \mathscr{R}\ x$,则$x \in [x]$, 即每个元素$x$都属于自身的等价类$[x]$ ,因此所有等价类必将没有遗漏地覆盖$A$中每个元素,即所有等价类的并集是$A$本身.
再证互斥性:Two distinct equivalence classes are disjoint. (i.e. have no elements in common)
对不同的等价类$[a]$和$[b]$ , 假设$[a]$和$[b]$交集不为空,取交集中的一个元素$c$. 我们要推出$[a]=[b]$,用反证法证明$[a]$和$[b]$ 的交集为空。
因为$c \in [a]$ 且 $c \in [b]$ , 有 $c\ \mathscr{R}\ a$ 且 $c\ \mathscr{R}\ b$ . 由等价关系的对称性和传递性有$a\ \mathscr{R}\ b$.
假设$x \in [a]$ ,有$x\ \mathscr{R}\ a$. 由传递性有$x\ \mathscr{R}\ b$ , 则$x \in [b]$ . 所以$[a] \subseteq [b]$ .
类似地,假设$x\in [b]$ 可以推出$[b] \subseteq [a]$. 所以有$[a]=[b]$.
这与$[a] \neq [b]$ 矛盾,所以假设不成立,即不同的等价类交集为空. $\square$
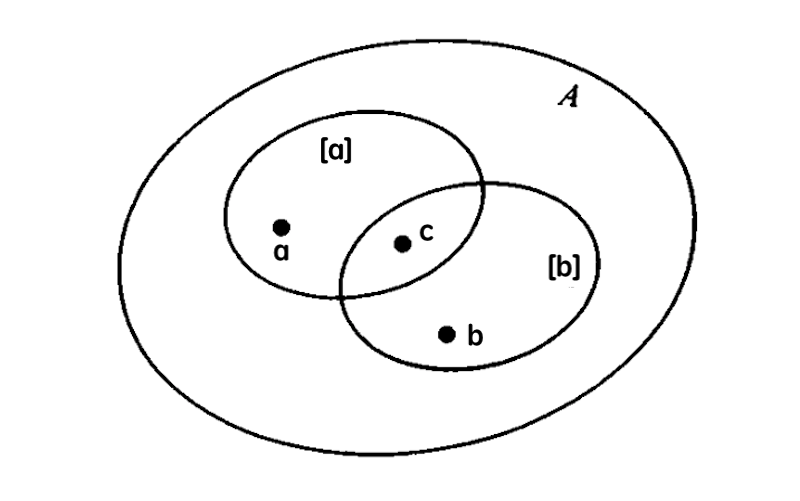
划分的唯一性 $A$中的每个元素$a \in A$ 只能属于一个等价类.
Proof. ($i$) 先证每个$a \in A$ 都至少属于一个等价类: 根据等价关系的自反性,$\forall a \in A$, 有$a\ \mathscr{R}\ a$ ,即$A$中的每个元素都与自身存在等价关系,所以每个元素$a$都至少属于它自身的等价类$[a]$.
$(ii)$ 再证没有元素可以属于两个不同的等价类:上文已证明不同等价类的互斥性.
所以$A$中每个元素只能属于一个等价类. $\square$
进一步地,我们有:
命题 $a\ \mathscr{R}\ b$ $\iff$ $[a]=[b]$
Proof. 先证”$\impliedby$” : 假设$[a]=[b]$ . 因为$a\ \mathscr{R}\ a$ ($\mathscr{R}$是自反的),我们有 $a \in [a] = [b]$ . 由$a \in [b]$ 知 $a\ \mathscr{R}\ b$.
再证”$\implies$”:假设$a\ \mathscr{R}\ b$. 先证$[a] \subseteq [b]$: 取任意$x \in [a]$ ,有$a\ \mathscr{R}\ x$. 由对称性有$x\ \mathscr{R}\ a$. 因为$x\ \mathscr{R}\ a$且$a\ \mathscr{R}\ b$ ,由传递性有$x\ \mathscr{R}\ b$ ,所以$x \in [b]$. 所以有$[a]\subseteq [b]$.
再证$[a]\supseteq [b]$. 取任意$x \in [b]$ ,有$b\ \mathscr{R}\ x$. 因为$a\ \mathscr{R}\ b$ 且 $b\ \mathscr{R}\ x$ ,由传递性有$a\ \mathscr{R}\ x$ ,所以有$x \in [a]$ . 所以$[b]\subseteq [a]$. 即$[a]\supseteq [b]$ . 所以$[a]=[b]$ . $\square$
