Question: 什么情况下两个集合$A$和$B$的大小相同?
Answer: 如果两个集合中的元素可以一一配对,则两集合的的大小相同。(Theory of Cardinality By Cantor)
举个例子来理解:假设你是一个对数字完全没有概念的原始人,你有一群猪和一群羊,但还没学会数数,如何判断猪和羊的数量是否相等呢?把猪全部赶进一个圈子(集合A),再把羊全刚进另一个圈子(集合B),然后把猪和羊逐个出来排队,两队并列进行一一配对,如果每头猪刚好能配一只羊,我们就说猪和羊的数量是相等的。(两集合的基数相等)
为了准确地描述这种“一一对应”关系,我们需要先定义函数/映射。
基于集合论的非正式定义
从集合$A$到集合$B$的函数$f$是一个映射,它为 $\forall x \in A$ 分配一个唯一的$y \in B$ . 记为$f:A \to B$ .
举个例子,从$S := {0,1,2}$ 到 $T := {0,2}$ 的函数$f:S\to T$ 可以通过$f(0):=2$, $f(1):=2$ 和$f(2):=0$ 的赋值操作来定义。也就是说,函数$f:A\to B$ 可被看成一个黑盒,我们输入一个$A$中的元素就会输出一个$B$ 中的元素。函数 $f$ 有时也被叫做映射 (a mapping or map),我们说$f$把$A$映射到$B$.
函数经常通过某个公式来定义,然而你应该仅把函数看作一个非常大的值表 (指将变量的取值和函数值对应起来的表格). 原因在于同一个函数可以有多种不同的公式表示,而且绝大多数函数是写不出表达式的,只能用表格或曲线图形来表示。
注意:我们讨论的函数(映射)只考虑一对一或多对一关系,即一个$A$中的元素不可以与多个$B$ 中的元素对应。一对多关系可以用“多值函数”表示,通常我们规定一对多不是映射,因为任何一对多关系的映射都可以直接转化为一对一的关系,只需把这多个元素塞进一个新集合里,这个集合里的元素就是从该输入可能得到的所有输出。
严格的函数定义:笛卡尔积的子集
笛卡尔积(Cartesian product)的定义 设$A$、$B$ 为集合. 笛卡尔积是定义为
\[A \times B := \lbrace (x,y) \mid x \in A, y \in B\rbrace\]的二元组的集合 (set of tuples). 例如 $\lbrace a,b\rbrace\times \lbrace c,d \rbrace= \lbrace (a,c),(a,d),(b,c),(b,d)\rbrace$ .一个更复杂的例子是集合$[0,1]\times [0,1]$,这是平面的一个子集:被顶点为$(0,0),(0,1),(1,0),(1,0)$ 的正方形所围成。当$A$和$B$是相同的集合,我们常用上标$2$来表示这样的乘积。例如 $[0,1]^2 = [0,1]\times[0,1]$ 或 $\mathbb{R}^2 = \mathbb{R}\times\mathbb{R}$ (笛卡尔直角坐标平面)
函数的严格定义 函数$f: A\to B$ 是$A\times B$ 的一个子集,集合$f$中的有序对 $(x,y)\in f$满足:
对每个$x \in A$ , 都存在唯一的$y\in B$ 与之对应,记为$f(x)=y$ .
(不能出现两个有序对具有相同的第一个元 $(x,y_1) \in f\ \wedge (x,y_2) \in f \implies y_1=y_2$ )。
有时把这个有序对的集合$f$ 称为函数的图像 (graph) 而不是函数本身。
集合$A$称为函数$f$的定义域(domain) ,有时记为$D(f)$. 集合
$R(f) := \lbrace{ y \in B \mid \exists\ x \in A\ s.t. f(x)=y \rbrace}$ $= \lbrace f(x)\in B \mid x \in A \rbrace$ 称为函数$f$的值域(range).
集合$B$称为函数$f$的陪域. 值域$R(f)$ (这里指定义域在$f$下的像$f(A)$ )可能是陪域$B$的真子集 (与$B$不相等). 而定义域总是指$A$. 我们通常假设$f$ 的定义域不为空。
像与逆像
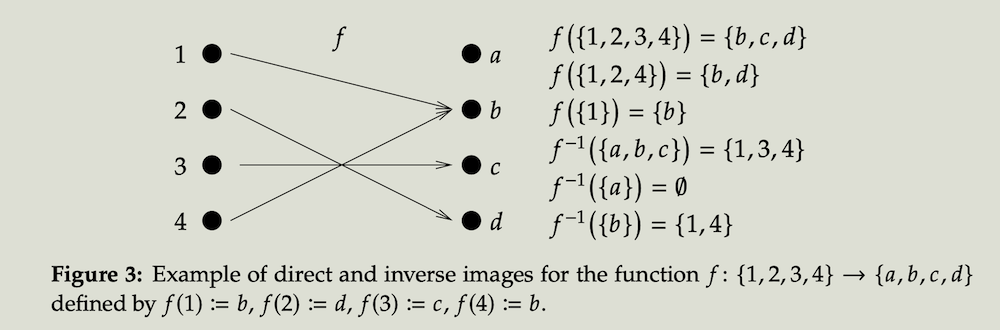
像(image)的定义 考虑函数$f:A\to B$ ,定义域的子集$C \subseteq A$的像 (image或direct image) 定义为
\[f(C)=\lbrace f(x) \in B \mid x \in C\rbrace\]陪域$B$的子集$D\subseteq B$ 的逆像 (inverse image, 也叫原像)定义为
\[f^{-1}(D) = \lbrace x \in A \mid f(x) \in D\rbrace\]特别地,有$R(f)=f(A)$ ,即这里函数的值域就是指定义域$A$的像(image) 。
像与逆像举例 定义函数$f:A\to B$ 为$f(x) := \sin (\pi x)$ . 则有
则有$f([0,\frac{1}{2}])=[0,1]$ ,$f^{-1}({0})=\mathbb{Z}$ 等等.
与逆像有关的命题 考虑函数$f:A\to B$ . 令$C$ 和 $D$为$B$ 的子集, 则
\[\begin{align} (1)& \quad f^{-1}(C\cup D) = f^{-1}(C) \cup f^{-1}(D) \\ (2)& \quad f^{-1}(C\cap D) = f^{-1}(C) \cap f^{-1}(D) \\ (3)& \quad f^{-1}(C^{\complement}) = (f^{-1}(C))^{\complement} \end{align}\]命题$(3)$ 应理解为 $f^{-1}(B-C) =A - f^{-1}\left(C\right)$ .
Proof. 根据逆像、交并补运算的定义可推出“$\subseteq$” 和 “$\supseteq$”关系成立,从而证明集合相等. 证明过程类似,此处略。
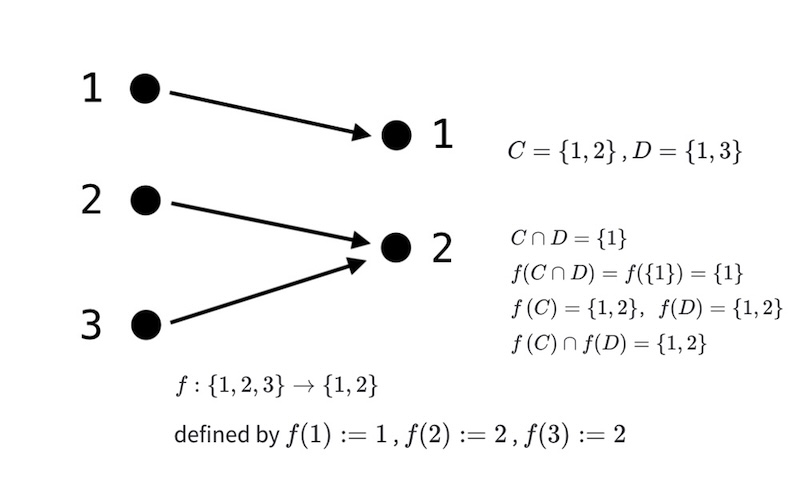
与像有关的结论更弱一些 (交集的像不一定等于像的交集):
与像有关的命题 考虑函数$f:A\to B$ . 令$C$ 和 $D$为$A$ 的子集, 则
\[\begin{align} (4)& \quad f(C\cup D) = f(C) \cup f(D) \\ (5)& \quad f(C\cap D) \subseteq f(C) \cap f(D) \end{align}\]Proof. 根据定义容易证明$(4)$ 等式成立. $(5)$ 根据定义容易证明“$\subseteq$” 成立,反之则不成立, 仅当$f$是单射时左右两个集合才相等. 当$f$不是单射(存在多对一关系)时,可能出现两子集交集的像小于各自像的交集,甚至$C\cap D$为空集的情况.
反例1 定义$f:\mathbb{N} \to {0,1}$ 为 $f(x) = x \ \text{mod}\ 2$ . 令 $C = {2, 4}$ , $D={1, 6}$ . 则
$C\cap D = \emptyset$ , $f(C\cap D)=\emptyset$ , $f\left(C\right)={0}$, $f(D)={0,1}$ ,$f\left(C\right)\cap f(D)={0}$
反例2 令$𝐶=\lbrace 1,2 \rbrace$, $𝐷=\lbrace 1,3\rbrace$ ,设 $𝑓(1)=1$, $𝑓(2)=2$, $𝑓(3)=2$
单射、满射、双射、反函数、复合函数
单射的定义 令$f:A\to B$ 表示一个函数。如果
\[f(x_1) = f(x_2) \implies x_1 = x_2 \quad \Bigl(\ x_1 \neq x_2 \implies f(x_1)\neq f(x_2)\ \Bigr)\]我们就称$f$是单射的 (injective) 或一对一的 (one-to-one) 。换句话说,如果对陪域$B$中每个元素 $\forall y \in B$ , 逆像$f^{-1}({y})$ 只包含一个元素或者为空,则我们称$f$是单射函数( injection或 injective function ).
如果$f(A)= B$,则我们称$f$是满射的(surjective) 或映成的(onto). 换句话说,如果$f$的值域与陪域是相等的,我们就称$f$是满射函数 (surjection).
如果$f$即是单射又是满射,则我们称$f$是双射的(bijective) 或 $f$是满射函数 (bijection).
当$f:A\to B$ 是双射函数时,$B$ 中每个元素的逆像 $f^{-1}({y})$ 总是$A$ 中一个唯一的元素. 我们把$f^{-1}$看作一个函数$f^{-1}:B \to A$ , 简写为$f^{-1}(y)$ . 此时我们称$f^{-1}$ 是$f$的反函数 (逆函数,inverse function). 注意,仅当$f:A\to B$为双射时,反函数才存在. 例如,对于由表达式$f(x):=x^3$ 定义的双射函数$f:\mathbb{R}\to\mathbb{R}$ ,我们有$f^{-1}(x)=\sqrt[3]{x}$ .
复合函数的定义 考虑函数$f:A\to B$ 和函数 $g:B \to C$. 函数$f$和$g$ 的复合函数 (composition of functions)
$g\circ f: A\to C$ 定义为:
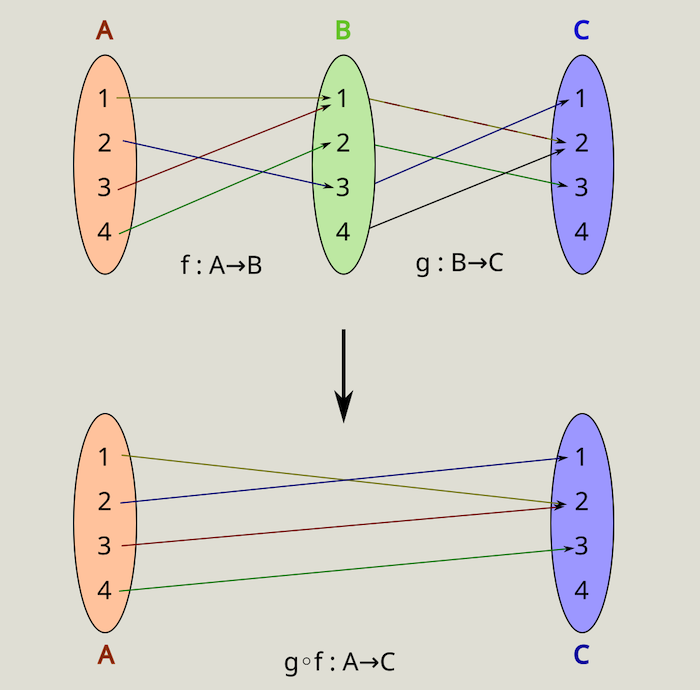
例如,如果函数$f:\mathbb{R}\to\mathbb{R}$ 是 $f(x) := x^3$ 且函数$g:\mathbb{R}\to\mathbb{R}$ 是$g(y):=\sin(y)$ ,则复合函数$(g\circ f)(x) = \sin(x^3)$ .
命题 双射函数的复合函数还是双射函数 (composition of bijections is a bijection)
Proof. 令$h:A\to C$ 是双射函数$f:A\to B $ 和 $g:B\to C$ 的复合函数,记为$h(x)=(g\circ f)(x)$ .
先证$h$是单射,即$h(x_1)=h(x_2) \implies x_1 = x_2$ .
如果$h(x_1)= h(x_2)$ 则有
$g(f(x_1))=g(f(x_2))$ $\implies$ $f(x_1)=f(x_2)$ (g是单射) $\implies$ $x_1=x_2$ (f是单射). $h$是单射得证.
再证$h$是满射, 即$h(A)=C$ : $\forall z \in C,\ \exists\ x \in A\ s.t.\ h(x)=z $.
令$z \in C$. $\because g$是满射 $\therefore $ $\forall z \in C,\ \exists\ y \in B \ s.t.\ g(y)=z$.
$\because f$是满射 $\therefore$ $\forall y \in B,\exists x \in A\ s.t. f(x)=y$
$\therefore$ $\forall z \in C,\ \exists x \in A\ s.t.\ g(f(x))=z$ 即 $h(x)=z$ . $h(A)=C$ 得证. $\square$
