基数 Cardinality
基数(可理解为集合的大小,size of sets) 这个概念常常让初学者产生困惑. 在现代数学尤其是数学分析中,基数的概念很重要.
基数的定义
设$A$和$B$ 为集合. 如果存在双射函数$f:A\to B$ ,我们就说$A$和$B$有相同的基数 (cardinality) 或$A$与$B$ 是等势的(equinumerous).
我们把与$A$有相同基数的所有集合的等价类记为$|A|$ .我们把$|A|$称为集合$A$的基数.
例如,$\lbrace 1,2,3 \rbrace$ 与${a,b,c}$有相同的基数,因为我们可以定义双射函数:$f(1):=a$ , $f(2):=b$,$f(3):=c$ . 显然两个集合之间可以构造的双射函数不是唯一的.
两个集合之间双射函数的存在其实是一种等价关系. 由公式$f(x):=x$ 定义的双射函数体现了自反性; (双射$f:A\to A$存在,即集合$A$与自身有相同基数). “如果$f$是双射函数,则$f^{-1}$也是双射函数” 体现了对称性;“如果$f:A\to B$ 和 $g:B\to C$ 都是双射函数,则$g\ \circ f: A\to C$ 也是双射函数” 体现了传递性. 一个集合$A$与空集有相同的基数当且仅当$A$本身就是空集. 如果$B$是非空的,则不存在形如$f:B\to \emptyset$ 的函数. 特别地,不存在从$B$ 到 $\emptyset$ 的双射函数.
有限集合与无穷集合
对某个$n \in \mathbb{N}$, 如果$A$与$\lbrace1, 2, 3, \cdots,n \rbrace$ 基数相同,我们把$A$的基数记为$|A|:=n$ . 如果$A$是空集则记为$|A|:=0$. 以上情况我们说$A$是有限 (finite) 的. 有限集的基数就是集合中元素的个数. 如果$A$不是有限的,即$A$包含无限个元素,我们说$A$是无限的(infinite)或者说$A$有无穷基数(of infinite cardinality).
根据以上定义我们有:如果对某个$n\in \mathbb{N}$ , 从集合$A$到$\lbrace1,2,3\cdots n \rbrace$ 存在一个双射函数,则$A$ 是非空有限集.
注:”For some $x$, $P(x)$” is the same as “there exists (at least one) $x$ such that $P(x)$”.
通过证明自然数$n$的唯一性,我们可以得到更强的结论:
命题 对每个非空有限集$A$,存在唯一的自然数$n$ 使得从$A$到$\lbrace1,2,3,\cdots,n \rbrace$ 存在一个双射函数.
Proof. 假设对某个$m \in \mathbb{N}$ ,存在另一个双射函数$g:A\to \lbrace 1,2,3\cdots, m\rbrace$ . 考虑$f^{-1}:\lbrace1,2,3\cdots,n\rbrace \to A$ 和 $g$ 的复合函数$g\ \circ f^{-1}: \lbrace{1,2,3\cdots, n\rbrace} \to \lbrace1,2,3,\cdots,m\rbrace$ . 因为$f^{-1}$和$g$ 都是双射函数,$g\ \circ f$ 也是双射函数,所以集合$\lbrace1,2,3,\cdots,n\rbrace$与$\lbrace1,2,3,\cdots,m\rbrace$有相同的基数,即元素个数相同,从而有 $n=m$, 唯一性得证. $\square$
我们可以根据基数(集合的大小) 来对集合进行排序。
序关系定义 如果从$A$ 到 $B$ 存在一个单射函数,我们就记作$|A| \le |B|$.
如果$A$和$B$有相同基数则记作$|A|=|B|$.
如果$|A|\le|B|$但$A$和$B$没有相同的基数,则记作$|A|\lt|B|$.
Cantor–Bernstein–Schröder定理 $|A| \le |B|$ 且 $|B| \le |A|$ $\iff$ 集合$A$和$B$有相同基数(等势).
另一种表述:如果集合$A$和$B$之间存在单射 $f:A\to B$ 和 $g:B\to A$ ,则存在一个双射$h:A\to B$.
康托尔-伯恩斯坦-施罗德定理的证明超出课程范围,这里不展开.
关于基数真正有趣的例子是无穷集合. 我们将区分两种不同的无穷基数.
可数无穷
如果$|A|=|\mathbb{N}|$ , 则我们说$A$是可数无穷的(countably infinite). 如果$A$是有限的或可数无穷的,我们说$A$是可数的(countable). 如果$A$不是可数的,则我们说$A$是不可数的 (uncountable) .
自然数集$\mathbb{N}$ 的基数通常记作$\aleph_0$ (读作aleph-naught, 阿列夫零).
一个无穷集合 (如有理数集$\mathbb{Q}$)是可数的,按照定义就是说能建立从自然数集$\mathbb{N}$到这个无穷集合的双射。从计数 (counting)的角度去理解, 也就是能无遗漏无重复地遍历集合中的元素。 由于自然数集$\mathbb{N}$ 可以从小到大顺序排成无穷序列$1,2,3,\cdots n\cdots$ ,一个无穷集合可数当且仅当集合中元素可以排成一个无穷序列$a_1,a_2,a_3,\cdots a_n\cdots$ (这就是无遗漏无重复的遍历)。如果一个集合是可列 (可数)的,那么它的每个元素与自然数的一一对应关系可以通过列表的形式无遗漏地列出来。(对角线法证明实数集不可数就用到了这个形式,Cantor发现总能找到至少一个列表之外的数,来说明这个列表不全)
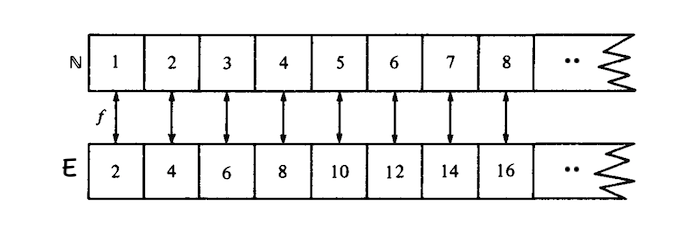
例1 正偶数集 (even natural numbers) 与自然数集$\mathbb{N}$有相同的基数.
Proof. 令$E \subset \mathbb{N}$ 为所有正偶数的集合. 给定$k \in E$ 都可表示为 $k = 2n$ ($n \in \mathbb{N}$) , 则存在由$f(n):=2n$ 定义的双射函数$f:\mathbb{N}\to E$ . $\square$
“自然数集能与它的真子集正偶数集建立一一对应” 是伽利略悖论 (Galileo’s paradox) 的一个版本 (原版是自然数集与自然数的平方的集合一一对应) . 伽利略及其同时代的科学家对此感到困惑,因为这与“整体大于部分”的直觉不符,他们认为两个无穷集合是无法比较大小的。这个悖论揭示了无穷集合的不同特征:有限集合的元素个数总是大于它的真子集,但无穷集合却可以与真子集中的元素一一对应。
事实上,这里我们不加证明地指出,无穷集合的特征就是:一个集合是无穷集当且仅当它能与自身的一个真子集构成一一对应. 这打破了统治数学界两千多年的《几何原本》中“整体大于部分”的公理。在无穷集合的世界里,康托尔的基数理论推翻了欧几里得提出的这个在有限集合中成立的直觉。
伽利略悖论的另一个版本以几何关系的形式呈现:伽利略在他的《两门新科学》中提出,两个不等长的线段AB与CD上的点可以构成一一对应。如图,

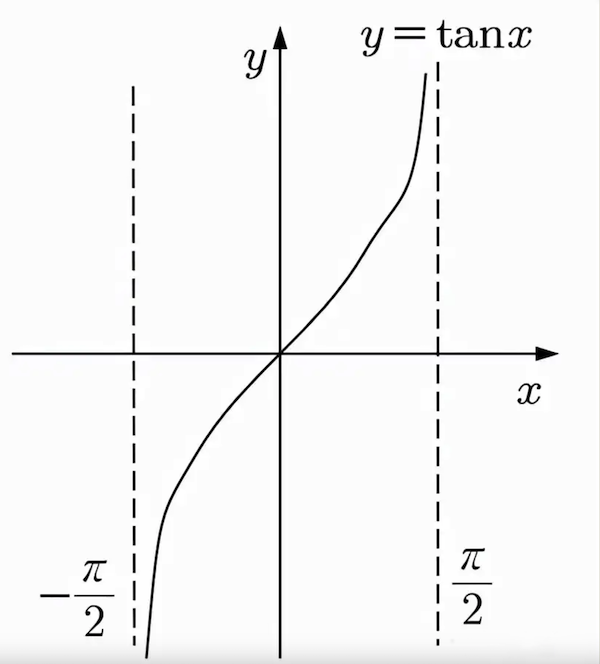
“不可数无穷集合与其真子集一一对应”有一个典型例子是三角函数$y=\tan x$ .
例2 $\mathbb{N} \times \mathbb{N}$ 是一个可数无穷集合.
Cantor定理
若$A$是集合,则$|A| \lt |\mathscr{P}(A)|$. 特别地,不存在从$A$ 到$\mathscr{P}(A)$ 的==满射函数==.
(换种说法:集合$A$与其幂集$2^A$ 不等势,即集合$A$与其幂集没有相同基数,基数总是小于其幂集)
Proof.
