引论
数学分析这门课的基础是 实数系的定义与性质，工科学生的高等数学课本往往没有这部分更基础的内容，而是从极限的定义或者数列开始。只有更深入地理解实数的性质，才能真正掌握极限这个既抽象又需要高度严谨性的概念。
实数的特殊之处
回顾我们从小到大学习数学的经历，可以发现我们所已知的「数」的范畴，是逐渐扩张与复杂化的。从幼儿园掰着指头数的$1,2,3$（自然数集 $N$), 到小学认识了分数与负数（扩张为有理数集Q）到第一次认识「无限不循环」的无理数$\pi$（扩张为实数$R$），以至于虚数单位的引入（扩张为复数$C$）…… 我们所认知到的数的形式越来越复杂，也越来越完善。这种从简到繁的认识过程，似乎十分符合自然规律。数学家 Kronecker（1823-1891）曾说过：「上帝创造了整数，其余的一切都是人为的。」自然数或者整数的概念，对于我们而言似乎是浑然天成的，几乎曾在地球上出现过的大多数重要文明都独立自主的掌握了关于自然数的概念；有理数略显复杂，但若是把所有有理数都看成两个整数之比$\frac{p}{q}$，则其也无非是自然数这一概念的延伸罢了。唯独由之更进一步的实数（更本质的说是实数中不是有理数的那一部分，即无理数），却并不那样显然；尽管我们可以举出像$\sqrt{2}$、$\pi$、$e$ 之类的数确实不能表示成两个整数之比，但对于是否有更多这样的数，它们又具有怎样的特性，我们并不清楚。
实数系特殊在哪里呢？它恰就特殊在其中出现了一种新的数: 无理数，而这一类数与「上帝创造的」整数之间的关系并不显然。特殊之处主要体现在以下几方面。
第一点，实数是不可列的。
有理数是可列的，有理数能与自然数建立双射。将有理数逐个列出的方法如下。有理数可以写成两个整数之比，分别以行和列将正整数排开，形成一个方阵的行标和列标，方阵的每个元素是行标与列标之比，表示一个正有理数，从1,1开始以对角线遍历方式即可遍历全部格点。说明有理数可以和整数能形成一一映射，是「一样多」的。
实数是不可列(不可数)的。 可通过康托对角线法反证得出。说明无理数比有理数要「多得多」。
考虑区间$[0, 1)$，假设它是可数的，用二进制表示来列出所有的数。此时构造一个数 $x$，它的第$i$位小数与$a_i$的第 $i$ 位小数相反，则 $x$ 不能被数到，矛盾。
第二点，实数比有理数更加「稠密」，实数具有「连续性」(没有空隙)。
不妨想一想，整数和有理数谁更稠密？答案当然是有理数，因为你可以挑出两个相邻的整数（如$n$ 与$n+1$），在它们之间找不出另一个整数；而在有理数中做不到，任何两个有理数之间都还存在着有理数，如果$a < b$是两个有理数，那么显然在它们之间的 $\frac{a+b}{2}$ 也是一个有理数。
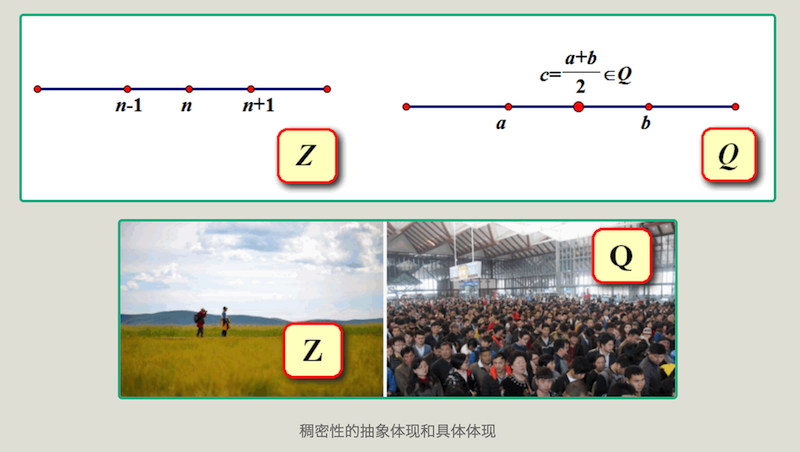
实数与有理数相比，谁更加「稠密」呢？显然实数集也满足所谓「稠密」的定义（毕竟有$Q \subset R$）；甚至我们把所有的有理数从实数集合中排除掉，只剩下无理数，也是满足这一「稠密」的要求的:
任意两个不同的无理数之间都还可以再找到一个无理数。（无理数集是稠密的）
证明： 取两个不相等的无理数$a < b$ , 它们的平均数 $\dfrac{a+b}{2}$ 显然在两数之间，但不一定是无理数。
如果$\dfrac{a+b}{2}$ 是无理数，命题显然成立。如果是一个有理数，即$\dfrac{a+b}{2} \in Q$ , 则$b$可以表示成 $r-a$ 的形式，其中$r$ 是一个有理数。 在a和b之间的线段上取右侧第一个四等分点, $a + \dfrac{3(b-a)}{4} = \dfrac{a}{4}+\dfrac{3b}{4} = \dfrac{a}{4}+\dfrac{3}{4}(r-a)=\dfrac{3}{4}r -\dfrac{a}{2} $ , 一定是无理数，因为这个数是有理数和无理数的和差形式。故任意两个不同无理数之间总能找到一个无理数，不是取中点，就是取四等分点。$#$
有理数集和实数集是不是同等稠密呢？显然不是。像我们之前所提到的$\sqrt{2}$、$\pi$、$e$ 等无理数，并不被「稠密」的有理数集所囊括 —— 换句话说，有理数这张「渔网」是有洞的，而且处处有洞。
如果把有理数集看成一个直线上的点集，为了补上这个点集中到处存在着的空隙，我们能不能通过添加更多的点来把空隙补满呢？答案是否定的，因为无理数集是不可数的, 不能与自然数集对等；我无法将其中的点一个一个列出来，自然也不可能通过向有理数集中一个一个「修修补补」的方法，把这些空隙填上。我们可以看到，有理数集向实数集拓张的过程中，发生了巨大的「转变」，这种转变比下图展示的还要剧烈。
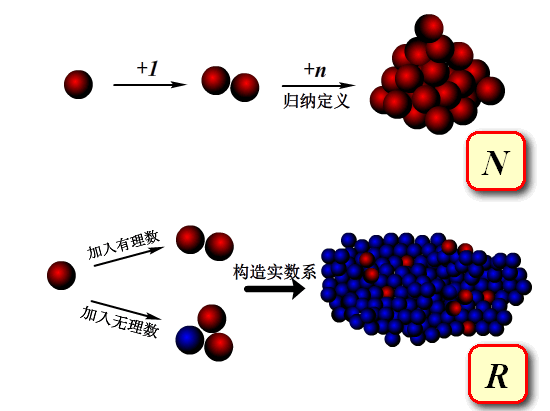
与实数集比起来，有理数集并没有那样稠密。实数集似乎有着比「每两个点中都有无穷多个点」更深刻、更高级的性质，使得它成为了一个连续 (没有空隙) 的点集，实数集的这种没有空隙的性质该如何描述呢？这个问题曾困扰了人类上千年，直到十九世纪末才得到比较圆满的解答。
第三点，有理数集对于极限运算是不封闭的，而实数集则对极限运算封闭。
当我们说某个数集对于某种运算封闭的时候，是指对于该数集中的任意一些数，经过该运算后得到的数仍在该数集中。例如，自然数集$N$ 对加法运算是封闭的（$\forall a, b \in N, a+b \in N$），而对于减法不封闭（例如$1 \in N,2 \in N, 1-2 = -1 \notin N$）。
有理数集$Q$对加减乘除四则运算都是封闭的，在数学上把具有这种性质的数系（数系包括数集和其上的运算）称为数域。 显然，实数集$R$也是一个数域。
既然有理数集对四则运算都是封闭的，那么无理数是如何由有理数运算得来呢？是天上掉下来的吗？这里可以举一个高等数学中计算「连续复利」的最基础例子：
\(\begin{align} \lim_{n \rightarrow \infty}(1+\frac{1}{n})^n = e \tag{1} \\ \end{align}\)
数列$a_n = (1+\frac{1}{n})^n$ 中的每一项都是有理数，但它却收敛到一个无理数, 或者说，它并不收敛于任何一个有理数。如果我们把极限看成一种对于有理数列的运算，那么这种运算对于有理数集是不封闭的。相反，实数中的任何一个收敛数列，却都一定收敛到实数集以内，不会出现「超实数」之类的更高级的数（也就是空隙）。这是有理数集与实数集最重要的差异之一；换句话说，实数集是完备的。
实数的构造理论
事实上，实数集所具有的这些特点，也曾经困扰过许多历史上著名的数学家，对于他们而言，自然数、整数、有理数都是十分自然的事物，而横空出世的无理数则令人困惑不已，如同怪物。古希腊的毕达哥拉斯学派则认为数就是有理数， 直到 $\sqrt{2}$ 被发现。
事实上，无理数是不可回避的概念，如同 $\sqrt{2}$ 这样的无理数之客观存在，表明这些数有它们存在的意义与价值。把实数集看成一根直线，任意取定一个原点和单位长度，上面便会有有理点和无理点的分别。有理数自然十分重要，然而没有无理数，这条直线就是不完整的。如果我们把直线上所有的无理点都刨去，那么一些我们完全可以利用有理点作出来的点竟然会不在这根直线上，这实在是荒谬不已。可以说，只有实数集才能反映我们眼前的真实世界，仅靠自然数、正负号和它们的比值是有缺漏的。
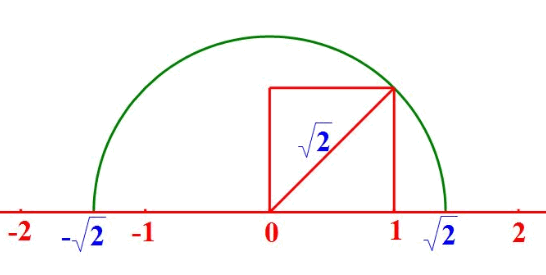
命题：边长为1的正方形的对角线长度不是有理数。
证明： 设边长为1的正方形对角线长度为$c$, 由勾股定理 $c^2 = 1^2 +1^2$ 即 $c^2 = 2$ 。下面用反证法证明。
假设 $c$ 是有理数，则 $c$ 可以表示为两整数之比$\dfrac{p}{q}$ , 其中$p$ 与$q$ 互素。
须满足 $(\dfrac{p}{q})^2 = 2$ 即 $p^2 = 2q^2$ 因为奇数的平方不可能是偶数，所以等式左边 $p$ 必为偶数。
令$p = 2s$ , $s$ 也为整数，有$(2s)^2 = 2q^2$ 即 $2s^2 = q^2$ 同理，$q$ 也必为偶数。
$p$ 和 $q$ 都为偶数，这与$p$ , $q$ 互素是矛盾的。故假设不成立，$c$ 不是有理数。 $#$
数学家们很早就意识到无理数是客观存在的数量中不可或缺甚至更加重要的一部分，却难以对无理数下一个清晰的定义。原因在于，无理数难以直接用已经存在的概念（特别是有理数）来定义。为什么一定要用存在的概念来定义呢？因为无理数同样是数，它也具有和当时人们已经基本上弄清楚的有理数相同的性质，比如可以加减乘除，表示直线上的点，等等。所以也理应将无理数看成「数」这个概念中不可分割的一部分。看作客观存在的东西，当然也要由客观存在的概念导出，而自然数的概念和由此推演而来的有理数的概念正是当时的人们所认为的客观成立的概念。所谓实数，正是指能够反映我们所处世界所有事物的数量情况的「数」的集合，这其中既有我们认为十分直观形象的有理数，也有性质非常模糊的无理数。实数是一个比自然数、有理数更高阶的概念，在完全弄清楚实数系所有性质以前，我们只能利用自然数、有理数的概念来定义实数，而绝不可能反过来（反过来是在此之后可以做的事情）。我们可以说自然数是一个我们已知的概念，我们不需要解释自然数究竟是什么（现今的数学家是以比「数」更加基本的概念 — 集合和元素来定义自然数的，详见Peano公理）。利用有理数构造无理数的方法，直到19世纪末才由一批杰出的数学家提出。
这些数学家是怎么利用有理数构造整个实数集的呢？不妨结合前文提到过的实数的三个特殊性质，来仔细想想。
实数集是不可数的。
实数的不可数性质能不能用来构造实数系呢？似乎不行，毕竟不可数并不是实数集特有的性质。不过，回想康托对角线法的证明过程，你也许会想起中学里面大家的老师曾经教过的一个概念：有理数是有限小数和无限循环小数，而无理数是无限不循环小数。这样解释的原因很简单，因为所有的分数都可以化为有限小数或者无限循环小数（注意分数都可以化为无限循环小数并不是一件显然的事情），而所有的有限小数和无限循环小数又都可以化为分数形式的有理数（这一点则比较显然）
命题：有理数就是有限小数或无限循环小数。
证明：先证有限小数或无限循环小数都可化为分数形式的有理数。 设一个无限循环小数的小数部分为：
\(\begin{align} a = 0.a_1a_2\cdots a_m\dot{b_1}\dot{b_2} \cdots \dot{b_n} \tag{*} \end{align}\) 其中$a_1a_2…a_m$表示不循环的部分，$\dot{b_1}\dot{b_2}…\dot{b_n}$表示循环的部分。只要小数部分能化为分数，无论整数部分是多少都能化为分数。有限小数可以看成循环部分$n = 0$ 的情况。$a$ 分别乘上$10^m$ 和 $10^{m+n}$ 得到：
此时发现它们的小数部分是一样的，$(2)-(1)$ 再除以系数得：
\(\begin{align} a = \frac{a_1a_2 \cdots a_mb_1b_2 \cdots b_n-a_1a_2 \cdots a_m}{10^m(10^n-1)} \tag{3} \end{align}\) 分子分母都是整数，从而我们就已经把无限循环小数化成分数，得证。反过来证明逆命题：所有的分数都可以化为有限小数或者无限循环小数, 只要证明所有分数都能通过通分化为分母是$10^m(10^n-1)$的形式，而由之前证明过程可知，这种形式的分数又必然对应着某个循环小数，要证的命题就等价于：
命题：对任意的正整数$k$, 至少存在一组正整数$m，n$, 使得$k$ 能整除$10^m(10^n-1)$
证明： $1, 10, 10^2,\cdots,10^k$ 这 $k+1$个数除以$k$ 的余数只可能是$0$到 $k-1$ 这 $k$ 个整数，由抽屉原理可知，这组数中必然存在两个不同的数除以$k$ 余数相同，不妨设这两个数为$10^i和10^j$（$i<j$）, 即至少存在一组正整数$i < j$, 使得$10^i\equiv 10^j \pmod k$ 。由同余的定义$10^i\equiv 10^j \pmod k$ 即 $10^j-10^i$ 能被 $k$ 整除。令$i = m, j-i = n$ , 则有$10^{m+n}-10^m = 10^m(10^n-1)$能被$k$整除。$#$
为什么戴德金分割（有理分割）构造出来的实数是连续的 (没有空隙)？
戴德金分割定理：对R的任一分割，B中必有最小的数（规定了左集A无最大值）。
说明了实数集没有空隙。 戴德金分割定理的证明见知乎杨树森的回答。