集合的记号
通常用大写字母来表示集合,例如$A, B, C, …,X,Y,Z$; 用小写字母表示集合中的元素,例如
$a,b,c,…x,y,z$. 我们使用$x \in S$ 这个特殊的记号来表示“$x$是集合$S$中的一个元素”、“$x$属于$S$” 。
如果$x$不属于$S$, 记为$x \notin S$。我们还可以把元素放在花括号中来表示集合,例如小于10的所有
正偶数集可记为$\lbrace2,4,6,8 \rbrace$ 所有正偶数集可记为$\lbrace 2,4,6\dots\rbrace$ 其中的“$\cdots$” 是“等等”(and so on)
的意思。 这种把集合的成员列在花括号中的表示方法也称为枚举法 (roster notation) 。
第一个集合相关的基本概念是集合的相等:
${\mathbf{集合相等的定义} }$ 如果集合A和集合B所包含的元素完全相同,那么我们称集合A
和集合B相等,记为$A=B$。如果其中一个集合包含了另一个集合中不存在的元素,
则称两个集合不相等,记为$A \ne B $ 。
${\mathbf{例子1}\ }$. 根据这个定义,集合$\lbrace 2, 4, 6, 8\rbrace$ 和集合 $\lbrace 2,8,6,4\rbrace$ 是相等的,因为它们都包含了2, 4, 6, 8
这4个元素。我们用枚举法来描述集合,集合与其中元素的顺序是无关的。
${\mathbf{例子2}\ }$ 集合 $\lbrace 2, 4, 6, 8\rbrace$ 和集合 $\lbrace 2,2,4,4,6,8\rbrace$ 是相等的,尽管在第二个集合中元素2和4被列举了
两次。两个集合都没有包含除了2, 4, 6, 8之外的元素,根据定义这两个集合也是相等的。这个例子
说明我们没有强制要求枚举法表示的集合中元素必须是互异的。另一个类似的例子是单词Mississippi
中字母的集合,与集合$\lbrace M,i,s,p \rbrace$ 相等,都包含了M, i, s, p这4个不同的字母。
子集
${\mathbf{子集的定义}\ }$ 如果集合A中的任意一个元素都属于B, 那么集合A称为集合B的子集,记为$A \subseteq B$,
也称“A包含于B”或“B包含A”。二元关系符$\subseteq$被称为“集包含” (set inclusion)
$A \subseteq B$ 这个命题并没有排除 $B \subseteq A$ 的可能性,仅当A和B中的元素完全相同时,
$A \subseteq B$ 和 $B \subseteq A$ 同时成立,即:
$\hspace{10em}$ $A = B$ 当且仅当 $A \subseteq B$ 且 $B \subseteq A$
如果$A \subseteq B$ 但 $A \ne B$ ,则我们称$A$ 是 $B$ 的真子集。记为$A \subset B$ 。
当我们应用集合论时,总是事先给定一个固定的集合S,而我们只关心这个给定集合的子集。集合S可以
根据不同的实际应用来确定,在每一段特定的论述中作为全集。 记号 $\lbrace \ x \ | \ x \in S \ 且 \ x 满足P \ \rbrace$ 表示集合S
中所有满足性质P的元素$x$ 。当全集$S$ 在上下文中已经明确时,我们可以简写为$\lbrace\ x\ |\ x 满足 P \ \rbrace$ ,读作
“所有满足性质P的 $x$ 的集合”。例如,所有正实数的集合可以记为$\lbrace\ x \ |\ x > 0\ \rbrace$ ,这种情形下默认全集S
是全体实数。类似地,所有正偶数的集合可以记为$\lbrace\ x \ |\ x 是一个正偶数\ \rbrace$。 当然,这里 $x$ 可以替换为其他
方便的记号,比如记为 $\lbrace\ x \ |\ x > 0\ \rbrace =\lbrace\ y \ |\ y > 0\ \rbrace=\lbrace\ t \ |\ t > 0\ \rbrace$。
一个集合中可能一个元素也没有,这样的集合称为空集,记为 $ \emptyset $ 。空集是任何集合的子集。
一些人把集合类比为包含着特定对象的容器 (比如背包或盒子)。 空集可以类比为一个空的容器。
为了避免逻辑困难,我们必须区分元素 $x$ 和集合 $\lbrace\ x\ \rbrace$ 。(装着一顶帽子的盒子和这顶帽子本身
在概念上是完全不同的)事实上,空集 $\emptyset$ 不含有任何元素,集合 $\lbrace\ \emptyset \ \rbrace$ 包含了 $\emptyset$ 这一个元素,
(包含了一个空盒子的盒子并不是空的) 由唯一一个元素构成的集合称为单元素集合 (one-element sets)。
图解有助于将集合之间的关系可视化。例如,可以把集合S看作平面内的一块区域,集合S中的每一个元素
即是一个点。那么S的子集就是区域内某些点的集合。这种图解叫做文氏图 (Venn diagrams) ,在集合论中
常用于检验定理的有效性或者为定理的证明方法提供一些启发。当然,证明本身必须完全基于概念的定义
而不是图解。
并集、交集、补集
给定集合$A$ 和 $B$ ,我们可以构造一个新的集合,称为$A$ 和 $B$ 的并集。这个新的集合记为
$A \cup B$ (读作:$A$ 并 $B$ )
并集就是把两个集合所有元素合并在一起组成的集合,定义为所有属于A或属于B的元素组成的集合,
即 $A \cup B = \lbrace x \ |\ x \in A \ 或\ x \in B \rbrace$ 也就是说$A \cup B$ 是至少属于A, B其中一个集合的元素的集合。
如图1.6(a)的阴影部分表示$A \cup B$
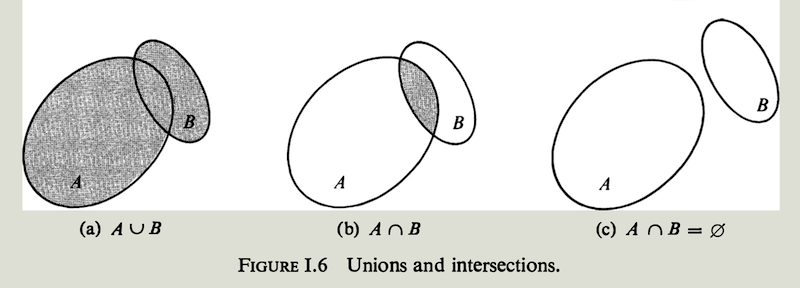
类似地,$A$ 和 $B$ 的交集记为 $A \cap B$ (读作:$A$ 交 $B$ )
定义为所有属于$A$ 且属于$B$ 的元素组成的集合,即 $A \cap B = \lbrace\ x \ |\ x \in A \ 且\ x \in B \ \rbrace$ 。
如图1.6(b) 的阴影部分所示。
图$1.6(c)$中两个集合$A$ 和 $B$ 没有共同的元素,此时它们的交集是空集 $\emptyset$ 。
如果$A \cap B = \emptyset$,则称集合$A$ 和 $B$ 是互斥 (disjoint) 的。
集合 $A$ 和 $B$ 的差集$A-B$ (也称为$B$ 在$A$中的相对补集)定义为属于 $A$ 但不属于 $B$ 的所有元素的集合,
即 $A - B = \lbrace x\ |\ x \in A \ 且 \ x \notin B \rbrace$。
图$1.6(b)$ 中区域$A$的非阴影部分表示$A-B$ ,区域B的非阴影部分表示$B-A$。
集合的交和并运算与普通的实数加法和乘法有许多形式上的相似之处,
例如根据定义,集合的交和并是顺序无关的,
因此集合的交和并运算满足交换律 (commutative),即
$A \cup B = B \cup A$ 以及 $A \cap B = B \cap A$。
根据定义交和并运算也满足结合律 (associative), 即
$(A \cup B) \cup C = A \cup (B \cup C)$ 以及 $(A \cap B) \cap C = A \cap (B \cap C)$
集合的交和并运算也满足分配律:
1)$A \cap(B \cup C)=(A \cap B) \cup (A \cap C)$
2)$A \cup (B \cap C) = (A \cup B ) \cap (A \cup C)$
1)证明:先证$A \cap(B \cup C) \subseteq (A \cap B) \cup (A \cap C)$.
对任意$x \in A \cap(B \cup C)$, 有 $x \in A$ 且 $x \in B \cup C$, 即:
$x \in A$ 且 ( $x \in B$ 或$x \in C$ )
若$x \in B$, 则 $x \in A$ 且 $x \in B$ 即$x \in A \cap B$
若$x \in C$, 则 $x \in A$ 且 $x \in C$ 即 $x \in A \cap C$
$\therefore$ 有 $x \in A \cap B $ 或 $x \in A \cap C$ 即 $x \in (A \cap B) \cup (A \cap C)$
由子集的定义,$A \cap(B \cup C) \subseteq (A \cap B) \cup (A \cap C)$ 得证.
再证$(A \cap B) \cup (A \cap C) \subseteq A \cap(B \cup C)$.
对任意$x \in (A \cap B) \cup (A \cap C)$, 有$x \in (A\cap B)$或$x\in (A\cap C)$ , 即:
$x \in A$ 且 ( $x \in B$ 或 $x \in C$ ) 即 $x \in A$ 且 $x \in B \cup C$
$\therefore$ $x \in A \cap (B \cup C)$. 由子集的定义,$A \cap(B \cup C) \subseteq (A \cap B) \cup (A \cap C)$ 也得证.
$\therefore$ 由集合相等的定义,分配律 1) 得证.
2)证明: 先证 $A \cup (B \cap C) \subseteq (A \cup B ) \cap (A \cup C)$.
对任意$x \in A\cup (B \cap C)$, 有$x \in A$ 或 $x \in B\cap C$, 即:
$x \in A$ 或 ( $x \in B$ 且 $x \in C$ )
若$x \in A$, 则有 $x \in A\cup B$ 且 $x \in A\cup C$
若$x \in B$ 且$x\in C$, 也有 $x \in A\cup B$ 且 $x \in A\cup C$
$\therefore$ 有 $x \in (A\cup B)\cap (A\cup C)$. 由子集的定义,$A \cup (B \cap C) \subseteq (A \cup B ) \cap (A \cup C)$ 得证.
再证$(A \cup B ) \cap (A \cup C) \subseteq A \cup (B \cap C)$ .
对任意$x \in (A \cup B ) \cap (A \cup C)$,有 ( $x \in A$ 或 $x \in B$ ) 且 ( $x \in A$ 或 $x \in C$ ) 成立,
若$x \in A$, 命题显然成立. 若$x \notin A$, 要使合取式的支命题同时为真,
须满足$x\in B$ 且 $x \in C$, 即$x \in B\cap C$.
$\therefore$ 有 $x \in A$ 或 $x \in B\cap C$ 即 $x \in A \cup (B \cap C)$.
由子集的定义,$(A \cup B ) \cap (A \cup C) \subseteq A \cup (B \cap C)$ 也得证.
$\therefore$ 由集合相等的定义,分配律 2) 得证.
集合的集合
集合的交和并运算可以推广到有限或无限集族 (Family of sets, 也叫collections of sets) 。
前面交集和并集定义在两个集合A和B之间,集族的交和并则定义在任意个集合之间。
为了简化语言,本书把集族称为类 (class)。设$\mathscr{F}$ 是一个包含集合的非空类。
类是一个比集合更广泛的概念。首先解释一下为什么要引入类。 曾经人们习惯于把满足某种条件的
对象的全体定义为集合,直到罗素发现了朴素集合论中的悖论,提出一个由不包含自身的集合所构成
的集合$S = \lbrace X| X \notin X \rbrace$ 从中推导出$ S \in S$当且仅当$S \notin S$ 的逻辑谬误。为了避免悖论,后来发展的
集合论公理系统通过增加分离公理和正则公理,从中可推出罗素集$S$不存在。 另一种解决方案是引入
“类”这个元语言符号来表示满足某条件的对象的全体,有些类是集合有些则不是,像罗素集这种不是集合
的类称为真类。可以认为类C和描述性质P的公式是同一个东西,x满足P可记为x属于C。S是一个真类,
用公式表示就是$不存在集合S, 使得\ \forall y, y \in S \iff P(y)$ ,即满足性质P的所有全体无法用集合来描述。
集族 $\mathscr{F}$ 中所有集合的并集被定义为至少属于其中一个集合的元素的集合,记为
\[\hspace{2em} \bigcup_{A \in \mathscr{F}}{A}\]如果 $\mathscr{F}$ 是一个有限集族,设 $\mathscr{F} = \lbrace A_1,\ A_2,\ \cdots A_n \rbrace$ , 则有${A}$
\[\bigcup_{A \in \mathscr{F}} A = \bigcup_{k\ =\ 1}^{n}A_k = A_1 \cup A_2 \cup \cdots \cup A_n\]类似地,集族 $\mathscr{F}$ 中所有集合的交集被定义为属于其中每一个集合的元素的集合,记为
\[\bigcap_{A \in \mathscr{F}} A\]同上,对于有限集族 $\mathscr{F}= \lbrace A_1, A_2, \cdots A_n \rbrace $ 有
\[\bigcap_{A \in \mathscr{F}} A = \bigcap_{k\ = 1}^{n} A_k = A_1 \cap A_2 \cap \cdots \cap \ A_n\]根据以上定义,任意个集合之间的交和并运算自动满足结合律。
