积分学的历史背景
阿基米德 (公元前287-212年) 的穷竭法演变成了今天的积分学。阿基米德曾用穷竭法求出圆的面积。
如图是穷竭法的举例,用内接多边形近似半圆的面积。

用穷竭法求抛物线下的面积
如图I.3所示,由抛物线$y = x^2$ 和两条直线$y=0, x= b$ 围成的图形称为一个抛物线段 (parabolic segment) ,
其面积设为A, 被一个底边长为b高为$b^2$ 矩形所包围。阿基米德发现抛物线下的面积正好是矩形的$1/3$ , 即
$A = b^3 /3$ 。我们来看看这个结果是如何推导出来的。
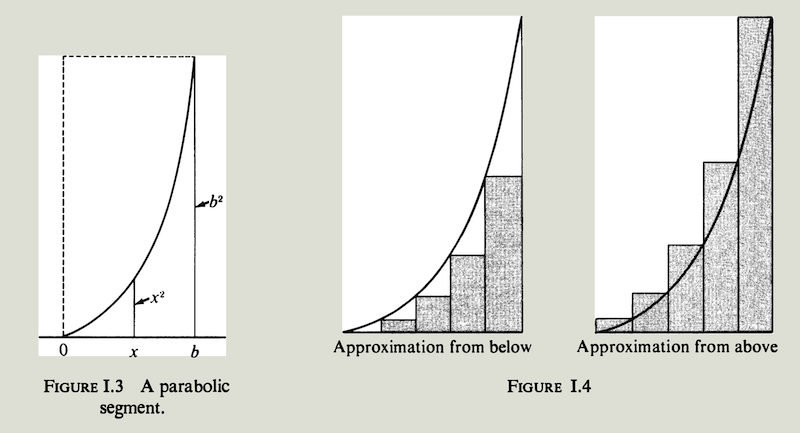
穷竭法的思想很简单,如图I.4所示,通过对底边进行划分,可以得到一系列的长条矩形,用矩形
面积之和来近似抛物线段的面积。内接矩形之和是面积A的一个下限,外接矩形之和是面积A的一个
上限。 随着划分越来越细,内接矩形的数量会越来越多,总面积会逐渐增大,外接矩形的数量也会
越来越多,总面积逐渐减小,总面积都会越来越接近抛物线段面积A。
如图I.5所示, 简单起见我们把底边n等分,每个长条矩形底边长为$b/n$ , 则等分点的横坐标x分别为:
一般地,$x = \dfrac{kb}{n}, \ k= 0,1,2,\cdots n$ . 则第 $k$ 个矩形的面积为$\left( \dfrac{b}{n} \right)\left( \dfrac{kb}{n} \right)^2=\dfrac{b^3}{n^3}k^2 $
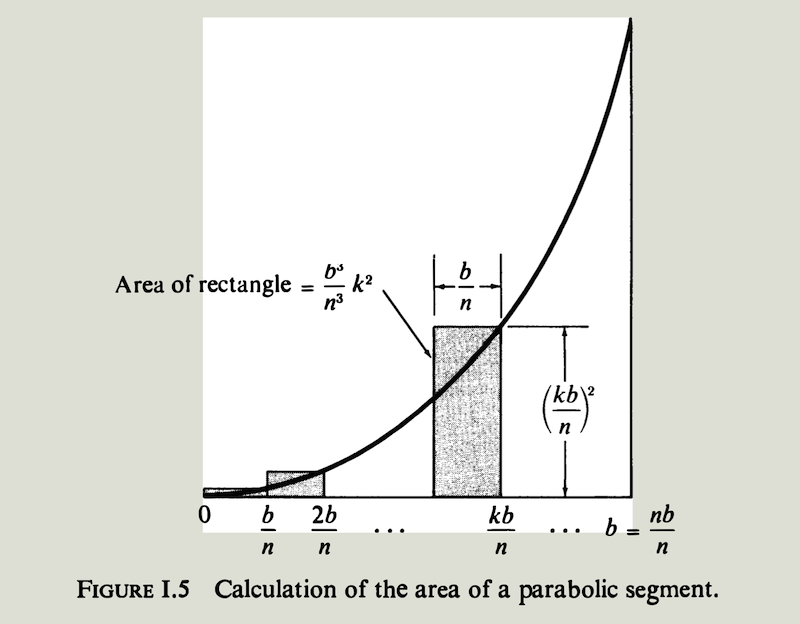
记外接矩形面积之和为$S_n$ ,其高度对应的横坐标 $x = \dfrac{kb}{n}, \ k= 1,2,\cdots n$ . 代入矩形面积表达式得
\(\hspace{-10em} \begin{align} S_n = \frac{b^3}{n^3}(1^2 + 2^2 + \cdots + n^2) \tag{1} \end{align}\)
记内接矩形面积之和为$s_n$, 其高度对应的横坐标 $x = \dfrac{kb}{n}, \ k= 0,1,2,\cdots n-1$ . 代入矩形面积表达式得 \(\hspace{-10em} \begin{align} s_n = \frac{b^3}{n^3}[1^2 + 2^2 + \cdots + (n-1)^2] \tag{2} \end{align}\)
下面来推导前n个自然数的平方和$1^2 + 2^2 + \cdots +n^2$ 的计算公式:
\(\hspace{-10em} \begin{align} 1^2+2^2+\cdots+n^2 = \frac{n^3}{3} + \frac{n^2}{2} + \frac{n}{6} \tag{3} \end{align}\)
这个公式对所有$n \ge1$ 均成立。证明过程如下。
把等式$(k+1)^3 = k^3+3k^2+3k+1$ 重写为 $3k^2+3k+1 = (k+1)^3-k^3$
代入$k=1,2,\cdots n-1$, 得到$n-1$个等式
\(\begin{align} 3 \cdot 1^2 + 3 \cdot 1 + 1 = 2^3 - 1^3 \\ 3 \cdot 2^2 +3 \cdot2 + 1 = 3^3 - 2^3 \\ \vdots \hspace{7em}\\ 3(n-1)^2 + 3(n-1) + 1 = n^3 - (n-1)^3 \hspace{-4em} \\ \end{align}\)
等号两边分别相加,等号右边消去剩下两项
\[\begin{align} 3[1^2 +2^2 + \cdots +(n-1)^2] + 3[1+2+\cdots+(n-1)] + (n-1) = n^3 - 1^3 \\ 3[1^2 +2^2 + \cdots +(n-1)^2] + 3\frac{n(n-1)}{2} + (n-1) = n^3 - 1^3 \\ 3[1^2 +2^2 + \cdots +(n-1)^2] = n^3 - 1^3 - 3\frac{n(n-1)}{2} - (n-1) \\ 1^2 +2^2 + \cdots +(n-1)^2 = \frac{n^3}{3} - \frac{1^3}{3} - \frac{n(n-1)}{2} - \frac{(n-1)}{3} \\ 1^2 +2^2 + \cdots +(n-1)^2 = \frac{n^3}{3} - \frac{n^2}{2} + \frac{n}{6} \tag{4} \\ \end{align}\]公式$(4)$ 两边加$n^2$ 就得到前n个自然数的平方和公式$(3)$
从公式$(3)$ 和 $(4)$ 可得到不等式
\(\begin{align} 1^2 +2^2 + \cdots +(n-1)^2 < \frac{n^3}{3} < 1^2+2^2+\cdots+n^2 \tag{5} \end{align}\)
对所有正整数$n \ge 1$ 都成立。两边乘$b^3/n^3$ 由$S_n$ 和$s_n$ 的公式$(1)$ 和 $(2)$ 可得不等式:
\(\begin{align} s_n < \frac{b^3}{3} < S_n \tag{6} \end{align}\)
对所有正整数$n \ge 1$ 都成立。 不等式$(6)$ 告诉我们 $b^3/3$ 是抛物线段面积A的下限$s_n$ 和上限$S_n$ 之间的一个数。
下面来证明$b^3/3$是满足这个不等式的唯一数字。也就是说,假设数字 $A$ 满足不等式
\(\begin{align} s_n < A < S_n \tag{7} \end{align}\)
那么 $A=b^3/3$ 。阿基米德就是据此得到抛物线段面积等于$b^3/3$ 这个结论。
在不等式$(5)$ 的左边部分两边加 $n^2$ 得:
\(\begin{align} 1^2 +2^2 + \cdots +(n-1)^2 + n^2 < \frac{n^3}{3} + n^2 \end{align}\)
两边同乘$b^3/n^3$, 由$S_n$ 的公式$(1)$ 得:
\(\begin{align} S_n < \frac{b^3}{3} + \frac{b^3}{n} \tag{8} \end{align}\) 类似地,在不等式$(5)$ 的右边部分两边减 $n^2$ ,再同乘 $b^3/n^3$ , 由 $s_n$ 的公式 $(2)$ 得:
因此,任何满足不等式 $(7)$ 的数字A也必须满足 $(8)$ 和 $(9)$ , 即
\(\begin{align} \frac{b^3}{3} - \frac{b^3}{n} < A < \frac{b^3}{3} + \frac{b^3}{n} \tag{10} \end{align}\)
对所有正整数$n \ge 1$ 都成立。$A$ 的取值有以下三种可能性:
\[\begin{align} A > \dfrac{b^3}{3}, \ A < \dfrac{b^3}{3},\ A = \dfrac{b^3}{3} \end{align}\]下面用反证法排除前两种可能性。
假设 $A > b^3/3$ 成立,由不等式$(10)$ 的右边部分,有
对所有正整数$n \ge 1$ 都成立。此时 $A - b^3/3$ 是正的, 不等式$(11)$ 两边同除以 $A - b^3/3$ 再同乘$n$得到:
\[\begin{align} n < \frac{b^3}{A - b^3/3} \end{align}\]对所有正整数$n \ge 1$ 都成立这个等价的不等式。当$n > b^3/(A-b^3/3)$ 时这个不等式显然是错误的,
与“所有正整数 $n \ge 1$ ”的成立条件矛盾,因此假设 $A > b^3/3$ 是不成立的,排除A的第一种可能性。
同理,假设 $A < b^3/3$ 成立, 由不等式$(10)$ 的左边部分,有
两边同除以 $b^3/3-A$ 再同乘$n$得到:
\[\begin{align} n < \frac{b^3}{b^3/3-A} \end{align}\]对所有正整数$n \ge 1$ 都成立这个等价的不等式。当$n > b^3/(b^3/3-A)$ 时这个不等式显然是错误的,
与“所有正整数 $n \ge 1$ ”的成立条件矛盾,因此假设 $A < b^3/3$ 是不成立的,排除A的第二种可能性。
所以 $A = b^3/3$ 原命题得证。
