1.20 单调函数与分段单调函数
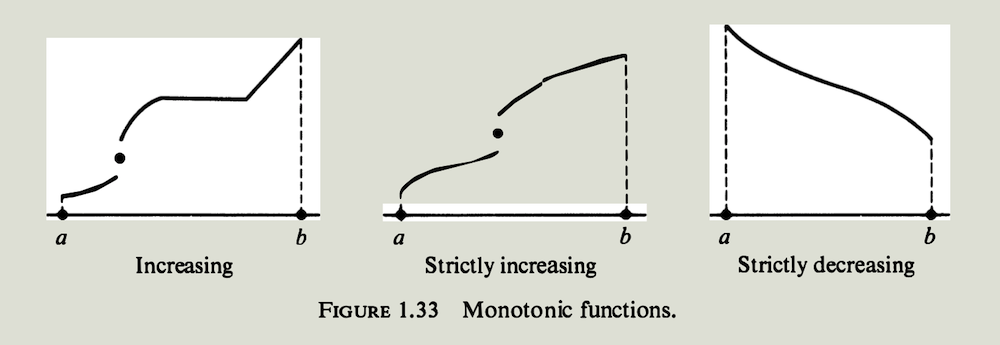
如果对集合$S$中$x<y$的每一对点$x$和$y$，都有$f(x) \le f(y)$ ，则称函数$f$在$S$ 上是递增的. 如果对$S$ 中所有$x\lt y$，严格不等式$f(x) \lt f(y)$ 成立，则称函数$f$在$S$上是严格递增的. 类似地，如果对$S$中所有$x\lt y$ 都有$f(x)\ge f(y)$ , 则称函数$f$在$S$上是递减的. 如果对$S$中所有$x\lt y$ 都有$f(x)\gt f(y)$ ，则称函数$f$在$S$上是严格递减的. 如果一个函数在$S$上递增或递减，则称函数在$S$上是单调的 (monotonic). 严格单调这个术语的意思是$f$在$S$上严格递增或严格递减. 通常我们讨论的集合$S$是一个开区间或是一个闭区间，例子如图$1.33$所示.
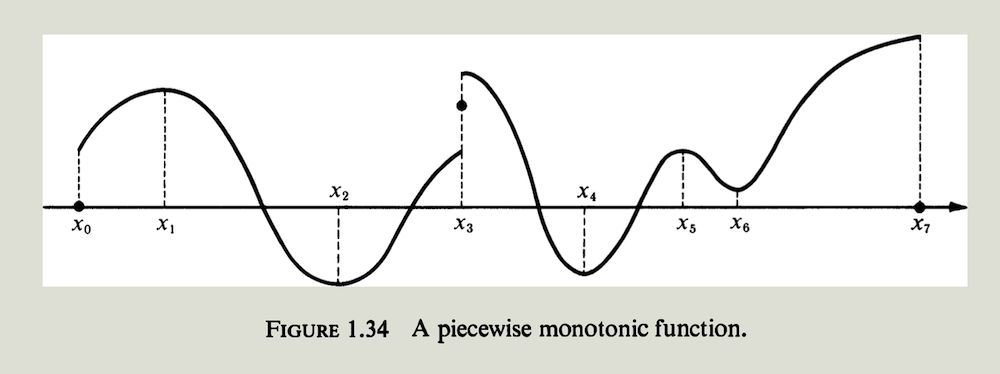
如果一个函数$f$的图像由有限个单调分段所组成, 则称函数$f$在区间上是分段单调的 (piecewise monotonic) . 也就是说，如果存在一个$[a,b]$ 划分$P$，使得$f$ 在$P$的每个开子区间都是单调，则$f$在$[a,b]$上是分段单调的. 特别地，阶梯函数就是分段单调的，如同图$1.33$和$1.34$所示的例子那样. 下面来看几个单调函数和分段单调函数的例子.
例1 幂函数 (power functions). 如果$p$是一个正整数，则对所有 $0\le x \lt y$ ，我们有不等式 \(x^p < y^p\) 成立. 以上结论由数学归纳法容易证得：当$p=1$时，$x\lt y$ 显然成立；假设对任意给定的正整数$k$，$x^k \lt y^k$ 成立.此时有$x^{k+1} = x^k \cdot x \lt y^k \cdot x < y^k \cdot y = y^{k+1}$ 即$x^{k+1} \lt y^{k+1}$. $#$ 这表明对于全体实数$x$， 由等式$f(x)=x^p$ 定义的幂函数在非负实轴上是严格递增的. 由数学归纳法和实数的序公理推论也容易证明： 幂函数$f$在负实轴上也是单调的. ($p$为偶数时递减，$p$为奇数时递增). 因此, 幂函数在每个有限区间是分段单调的.
例2 平方根函数 (square-root functions). 令$f(x)=\sqrt{x}$ ( $x \ge 0$ ). 这个函数在非负实轴上是严格递增的. 事实上，如果$0 \le x \lt y$ ，我们有 \(\sqrt{y}-\sqrt{x} = \dfrac{y-x}{\sqrt{y}+\sqrt{x}} \gt 0\) 即$\sqrt{x} < \sqrt{y}$ 成立.
例3 由$g(x)=\sqrt{r^2-x^2}$ ($-r \le x \le r$) 定义的函数$g$的图形是一个半径为$r$的半圆. 这个函数在区间$[-r,0]$上是严格递增的, 在区间$[0,r]$上是单调递减的. 因此$g$在$[-r,r]$上是分段单调的.
1.21 单调有界函数的可积性
单调函数在积分理论中之所以重要是因为以下定理.
定理1.12 如果有界函数$f$在闭区间$[a,b]$上是单调的，则$f$在$[a,b]$ 上是可积的.
证明： 我们先证明定理对于递增函数是成立的，递减函数的情况同理可证. 假设$f$是递增的. 令$\mathit{\underline{I}}(f)$和$\bar{I}(f)$分别表示$f$的下积分和上积分 (下阶梯函数积分的上确界和上阶梯函数积分的下确界) . 根据定理1.9，函数可积当且仅当上积分与下积分相等，因此我们只需证明$\mathit{\underline{I}}(f) = \bar{I}(f)$.
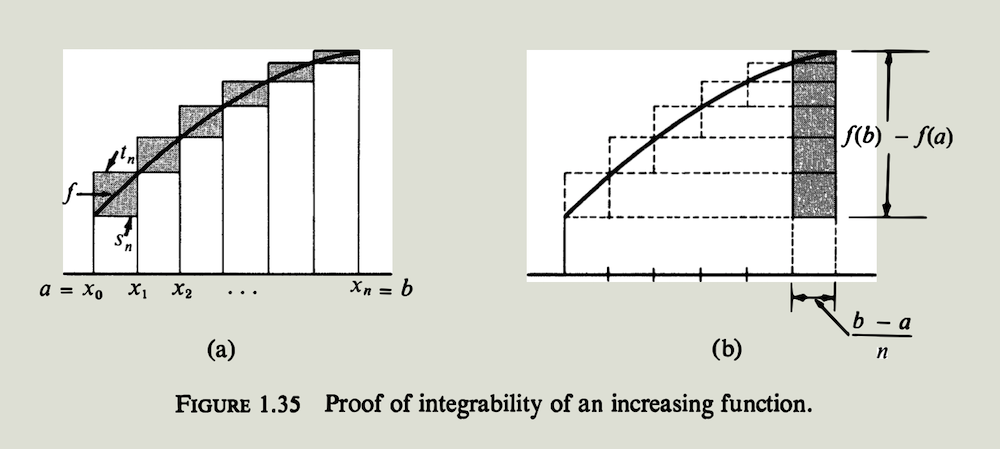
令$n$是一个正整数，构造两个特殊的近似阶梯函数$s_n$和$t_n$ : 令$P={x_0, x_1,\cdots,x_{n-1},x_n}$ 是一个把$[a,b]$等分成$n$个子区间的划分, 即每个子区间$[x_k, x_{k-1}]$的长度都为$x_k-x_{k-1}=\dfrac{b-a}{n}$. 现在用公式 \(s_n(x) = f(x_{k-1})\ , \quad t_n(x) = f(x_k) \quad (x_{k-1}\lt x \lt x_k)\) 来定义阶梯函数$s_n$和$t_n$. 在分点处，定义$s_n$和$t_n$的函数值使得在整个$[a,b]$上关系式$s_n(x) \le f(x) \le t_n(x)$ 成立. 如图$1.35$所示是一个例子. 关于构造出来的这两个阶梯函数，我们有
\[\begin{align} \int_a^b t_n - \int_a^b s_n &= \sum_{k=1}^n f(x_k) (x_k-x_{k-1})-\sum_{k=1}^n f(x_{k-1})(x_k-x_{k-1}) \\ &= \dfrac{b-a}{n}\sum_{k=1}^n [f(x_k)-f(x_{k-1})] \\ &= \dfrac{b-a}{n}(f(x_1)-f(x_0)+f(x_2)-f(x_1) + \cdots + f(x_n)-f(x_{n-1})) \\ &= \dfrac{b-a}{n} (f(x_n)-f(x_0)) = \dfrac{(b-a)[f(b)-f(a)]}{n} \end{align}\]最后一个等式描述的关系有一个简单的几何解释. $\int_a^b t_n - \int_a^b s_n$ 这个差等于图$1.35(a)$ 中阴影矩形面积之和. 把这些矩形滑动到右边，使它们落在一个共同的底上 (外阶梯区域第$n$个矩形的垂边上). 如图$1.35(b)$ 所示, 它们刚好填满一个底边长为$\dfrac{b-a}{n}$ , 高度为$f(b)-f(a)$ 的矩形, 所以阴影面积之和为$\dfrac{C}{n}$ , 其中$C = (b-a)[f(b)-f(a)]$.
现在我们把上述关系式重写为
\[\int_a^b t_n - \int_a^b s_n = \dfrac{C}{n} \tag{1.8}\]的形式. 因为$s_n \le f \le t_n$ 在$[a.b]$ 上成立，由阶梯函数积分性质之比较定理和上下确界的定义可知，$f$ 的下积分和上积分满足
\[\int_a^b s_n \le \mathit{\underline{I}}(f) \le \int_a^b t_n \quad 和 \quad \int_a^b s_n \le \bar{I}(f) \le \int_a^b t_n\]这两组不等式. 用 $-1$乘第一组不等式右边部分得 $-\mathit{\underline{I}(f)} \le - \int_a^b s_n $ ，再加到第二组不等式右边部分上，我们有
\[\bar{I}(f) - \mathit{\underline{I}}(f) \le \int_a^b t_n - \int_a^b s_n\]由等式$(1.8)$ 和关系式 $\mathit{\underline{I}}(f) \le \bar{I}(f)$ (上下积分的定义)，我们得到
\[0 \le \bar{I}(f)-\mathit{\underline{I}}(f) \le \dfrac{C}{n}\]即$\mathit{\underline{I}}(f) \le \bar{I}(f) \le \mathit{\underline{I}}(f)+ \frac{C}{n} $ 对所有正整数$n \ge 1$ 成立. 根据阿基米德性质的推论(定理I.31), 我们有$\bar{I}(f)=\mathit{\underline{I}}(f)$，这就证明了$f$ 在$[a,b]$上是可积的.
1.22 单调有界函数积分的计算
定理$1.12$ 的证明不仅说明了单调递增的有界函数存在积分，也提出了一个计算积分值的方法，可用以下定理来描述.
定理1.13 假设$f$在闭区间$[a,b]$上的递增的. 令$x_k = a + k(b-a)/n$ ($k=0,1,\cdots,n$) . 对所有$n\ge1$ 的正整数, 如果$I$是满足不等式
\[\dfrac{b-a}{n}\sum_{k=0}^{n-1}f(x_k) \le I \le \dfrac{b-a}{n}\sum_{k=1}^n f(x_k) \tag{1.9}\]的任何一个数，则$I = \int_a^b f(x)dx$.
证明： 如同定理$1.12$的证明中描述的那样，令$s_n$和$t_n$ 是把$[a.b]$ 区间$n$等分得到的两个特殊的近似阶梯函数. 不等式$(1.9)$ 指出，对所有$n \ge 1$ 的正整数，有
\[\int_a^b s_n \le I \le \int_a^b t_n \qquad \tag{1}\]由有界函数积分的定义，积分$\int_a^b f(x)dx$ 也满足
\[\int_a^b s_n \le \int_a^b f(x) dx \le \int_a^b t_n \qquad \tag{2}\]$(2)$乘上$-1$得：
\[- \int_a^b t_n \le - \int_a^b f(x)\ dx \le -\int_a^b s_n \qquad \tag{3}\]$(3)+(1)$ 得：
\[-(\int_a^b t_n - \int_a^b s_n) \le I - \int_a^b f(x)\ dx \le \int_a^b t_n - \int_a^b s_n\]又根据等式$(1.8)$ 有
\[\left| I - \int_a^b f(x)\ dx \right| \le \dfrac{C}{n} \qquad \tag{4}\]如果$I > \int_a^b f(x)dx$ , $(4)$ 变为: $I - \int_a^b f(x)dx \le \frac{C}{n}$ . 此时因为$I - \int_a^b f(x)dx >0$, 由阿基米德性质，对任意实数$C$，存在正整数$n$ 使得 $n(I-\int_a^b f(x)dx) > C$ 即 $I-\int_a^b f(x)dx > \frac{C}{n}$ 与$(4)$ 矛盾.
如果$I < \int_a^b f(x)dx$, $(4)$ 变为：$\int_a^b f(x)dx - I \le \frac{C}{n}$. 此时因为$\int_a^b f(x)dx - I >0$ , 由阿基米德性质，存在正整数$n$ 使得$n(\int_a^b f(x)dx-I) > C$ 即 $\int_a^b f(x)dx - I > \frac{C}{n}$ . 这也与$(4)$ 矛盾.
所以，$I = \int_a^b f(x)dx$. $#$
同理，类似的论证可给出递减函数情况下对应定理的证明.
定理1.14 假设$f$在闭区间$[a,b]$上是递减的. 令$x_k = a+k(b-a)/n\ (k=0,1,2,\cdots,n)$. 对所有$n\ge 1$ 的正整数，如果$I$ 满足不等式
\[\dfrac{b-a}{n}\sum_{k=1}^n f(x_k) \le I \le \dfrac{b-a}{n}\sum_{k=0}^{n-1} f(x_k)\]则$I = \int_a^b f(x) dx$.
1.23 积分 $\int_{0}^b x^p dx \ (p为正整数)$ 的计算
为了说明定理$1.13$的用法，我们来计算积分$\int_{0}^b x^p dx$，其中$b>0$ 且$p$是正整数. 因为被积函数在$[a,b]$ 上有界且单调递增，所以这个积分是存在的.
定理1.15 如果$p$为正整数且$b>0$ ，我们有 \(\int_0^b x^p\ dx = \dfrac{b^{p+1}}{p+1}\)
证明： 在I.4.10节数学归纳法杂题13(c) 中我们证明了不等式
\[\sum_{k=1}^{n-1}k^p \lt \dfrac{n^{p+1}}{p+1} \lt \sum_{k=1}^n k^p\]对每个正整数$n$ 和 $p$ 都成立.
用$\dfrac{b^{p+1}}{n^{p+1}}$ 乘上这组不等式得到：
\[\dfrac{b}{n} \sum_{k=1}^{n-1}\left( \dfrac{kb}{n} \right)^p \lt \dfrac{b^{p+1}}{p+1} \lt \dfrac{b}{n} \sum_{k=1}^{n}\left( \dfrac{kb}{n} \right)^p\]对于$k=0,1,2,\cdots,n$ ，如果我们令$f(x)=x^p$ 和 $x_k = \dfrac{kb}{n}$ 则这组不等式可化为
\[\dfrac{b}{n} \sum_{k=0}^{n-1} f(x_k) \lt \dfrac{b^{p+1}}{p+1} \lt \dfrac{b}{n} \sum_{k=1}^{n} f(x_k)\]$f(x)=x^p$ 在$[0,b]$ 上单调递增，根据定理1.13 (单调有界函数积分的计算方法) ，这组不等式恰好是$(1.9)$ 在$f(x)=x^p ,\ a=0,\ I = \dfrac{b^{p+1}}{p+1}$ 时的情形，所以$\int_0^b x^p dx = \dfrac{b^{p+1}}{p+1}$. $#$
1.24 积分的基本性质
从积分的定义出发，不难推导出以下积分的性质. （证明见$1.27$节)
定理1.16 关于被积函数的线性性 如果$f$和$g$ 在$[a,b]$ 上都是可积的，则对于每一对常数$c_1$和$c_2$ ，$c_1f+c_2g$ 也是可积的. 而且我们有
\[\int_a^b [c_1f(x)+c_2g(x)]\ dx = c_1 \int_a^b f(x)\ dx + c_2\int_a^b g(x)\ dx\]注：利用数学归纳法，线性性能被推广成如下形式：如果$f_1, f_2,\cdots,f_n$ 在$[a,b]$ 上可积，则对所有实数$c_1,c_2,\cdots,c_n$，$c_1f1+c_2f2+\cdots+c_nf_n$ 也是可积的. 并且我们有
\[\int_a^b \sum_{k=1}^{n}c_kf_k(x)\ dx = \sum_{k=1}^{n} c_k\int_a^b f_k(x)\ dx\]定理1.17 关于积分区间的可加性 如果以下三个积分有两个积分存在，则第三个积分也存在. 并且我们有 \(\int_a^b f(x)\ dx + \int_b^c f(x)\ dx = \int_a^c f(x)\ dx\)
注：如果$f$在$[a,b]$上是单调的，在$[b, c]$上也是单调的，则积分$\int_a^b f$ 和 $\int_b^c f$ 都存在，所以$\int_a^c f$ 也存在，并且等于另外两个积分之和.
定理1.18 **平移不变性 ** 如果$f$在$[a,b]$上可积，则对每个实数$c$，我们有
\[\int_a^b f(x)\ dx = \int_{a+c}^{b+c} f(x-c)\ dx\]定理1.19 积分区间的扩大或缩小 如果$f$在$[a,b]$ 上可积，则对于每个实数$k \ne 0$ , 我们有
\[\int_a^b f(x)\ dx = \dfrac{1}{k} \int_{ka}^{kb} f(\dfrac{x}{k})\ dx\]注：在定理$1.18$ 和定理$1.19$，其中一个积分的存在蕴含着另一个积分的存在. 当$k=-1$时，定理$1.19$称为放射性.
定理1.20 比较定理 如果$f$和$g$在$[a,b]$ 上都是可积的，且对$[a,b]$内的每个$x$有$g(x)\le f(x)$ , 则我们有
\[\int_a^b g(x)\ dx \le \int_a^b f(x)\ dx\]定理$1.20$一个重要的特例是当对每个$x$ 都有$g(x)=0$ 时. 在这种情况下，定理指出如果在$[a,b]$上处处有$f(x)\ge 0$ ，则有$\int_a^b f(x)\ dx \ge 0$. 换句话说，非负函数具有非负的积分. 还能证明：如果严格不等式$g(x) < f(x)$ 对$[a,b]$内所有$x$都成立, 则对于它们的积分，同样的严格不等式也成立，但这个阶段不易给出证明.
在第5章中我们将讨论各种计算积分值的方法，这些方法无须利用定义. 然而，这些方法仅适用于少数的函数，对于大多数可积函数，积分的实际数值只能通过估计来得出. 这通常由阶梯函数或其他可以精确计算积分值的简单函数从上和从下逼近被积函数，然后应用比较定理来得到所求函数积分的近似值. 在第7章“函数的多项式逼近”中我们将对这种思想进行更充分的探讨.
1.25 多项式的积分 Integration of polynomials
在$1.23$节中，我们证明了幂函数的积分公式
\[\int_{0}^b x^p \ dx = \dfrac{b^{p+1}}{p+1}\]对$b > 0$ 和任意正整数$p$ 都成立. 这个公式对$b=0$也成立，因为此时积分限都为0. 利用定理$1.19$ , 我们可以证明积分公式对于负的积分上限也成立. 我们只要令定理$1.19$ 中$a = 0,\ b=-b,\ f(x)=x^p$ ，再取$k=-1$ 就得到
\[\begin{align} \int_{0}^{-b} x^p\ dx &= - \int_{0}^b (-x)^p \ dx = (-1)\int_{0}^b (-1)^p x^p\ dx \\ &= (-1)^{p+1}\int_{0}^b x^p\ dx = \dfrac{(-1)^{p+1}b^{p+1}}{p+1} = \dfrac{(-b)^{p+1}}{p+1} \end{align}\]这就证明了积分公式对负的积分上限也成立. 又根据积分区间的可加性(定理1.17)，我们有
\[\begin{align} \int_a^b x^p\ dx &= \int_{a}^{0} x^p\ dx + \int_{0}^b x^p\ dx \\ &= \int_{0}^b x^p\ dx - \int_{0}^{a} x^p\ dx \\ &= \dfrac{b^{p+1}}{p+1} - \dfrac{a^{p+1}}{p+1} \end{align}\]这就推广出更通用的积分公式
\[\int_a^b x^p\ dx = \dfrac{b^{p+1}-a^{p+1}}{p+1}\]对积分限为任意实数$a$和$b$ 以及任意非负整数$p$ 都成立.
有时特殊符号
\[P(x) \left|_a^b\right.\]被用来表示$P(b)-P(a)$ 这个差. 于是幂函数的积分公式也可以写成
\[\int_a^b x^p\ dx = \left. \dfrac{x^{p+1}}{p+1} \right|_a^b = \dfrac{b^{p+1}-a^{p+1}}{p+1}\]利用幂函数积分公式，再结合积分的线性性，我们可以计算出任意多项式函数的积分. 例如，为了计算积分$\int_1^3 (x^2-3x+5)\ dx $ , 我们先求每项的积分，然后把结果加起来. 于是我们有
\[\begin{align} \int_1^3 (x^2-3x+5)\ dx &= \int_1^3 x^2\ dx - 3\int_1^3 x\ dx + 5\int_1^3 dx \\ &= \left. \dfrac{x^3}{3} \right|_1^3 -3\cdot \left. \dfrac{x^2}{2}\right|_1^3 + 5 \cdot \left. x \right|_1^3 \\ &= \dfrac{3^3-1}{3}- 3 \cdot \dfrac{3^2-1}{2} + 5 \cdot (3-1) \\ &= \dfrac{26}{3} - 12 + 10 = \dfrac{20}{3} \end{align}\]更一般地，为了计算任意多项式的积分，我们可以逐项积分：
\[\int_a^b \sum_{k=0}^n c_k x^k \ dx = \sum_{k=0}^n c_k \int_a^b x^k \ dx = \sum_{k=0}^n c_k \dfrac{b^{k+1}-a^{k+1}}{k+1}\]我们也能对由不同多项式组成的更复杂函数进行积分. 例如，考虑积分$\int_0^1 | x(2x-1)|dx $ . 因为绝对值符号，被积函数不是一个多项式，然而考虑$x(2x-1)$ 的符号，我们可以把区间$[0,1]$分成两个子区间，在每个子区间上被积函数是一个多项式，当$x$从$0$变化到$1$时，乘积$x(2x-1)$在点$x=\dfrac{1}{2}$ 处改变符号. 当$0 < x < \dfrac{1}{2}$ 时乘积是负的，当$\dfrac{1}{2} < x < 1$ 时乘积是正的. 因此，利用积分的可加性我们有
\[\begin{align} \int_0^1 \left|x(2x-1)\right| dx &= \int_0^{1/2} \left|x(2x-1)\right| dx + \int_{1/2}^1 \left|x(2x-1)\right| dx \\ &= \int_0^{1/2} - [x(2x-1)] dx + \int_{1/2}^1 x(2x-1)dx \\ &= -\int_0^{1/2} x(2x-1) dx + \int_{1/2}^1 x(2x-1)dx \\ &= - (2 \int_0^{1/2}x^2 dx - \int_0^{1/2} x dx) +(2 \int_{1/2}^{1}x^2 dx - \int_{1/2}^{1} x dx)\\ &= \left.\dfrac{x^2}{2}\right|_{0}^{1/2} - 2\cdot \left.\dfrac{x^3}{3}\right|_{0}^{1/2} + 2\cdot \left.\dfrac{x^3}{3}\right|_{1/2}^{1} - \left.\dfrac{x^2}{2}\right|_{1/2}^{1} \\ &= \dfrac{1}{8} - \dfrac{1}{12} + 2(\dfrac{1}{3}-\dfrac{1}{24}) - (\dfrac{1}{2}-\dfrac{1}{8})\\ &= \dfrac{1}{8} - \dfrac{1}{12} + \dfrac{7}{12} - \dfrac{1}{2} + \dfrac{1}{8}\\ &= \dfrac{1}{4} \end{align}\]