1.16 更一般函数的积分
当$s$是阶梯函数时,我们已经定义了积分$\int_a^b s(x)\ dx$ , 这一节我们将定义更一般函数$f$的积分. 定义构造出来的积分将具有阶梯函数积分的所有性质 (见$1.13$节).
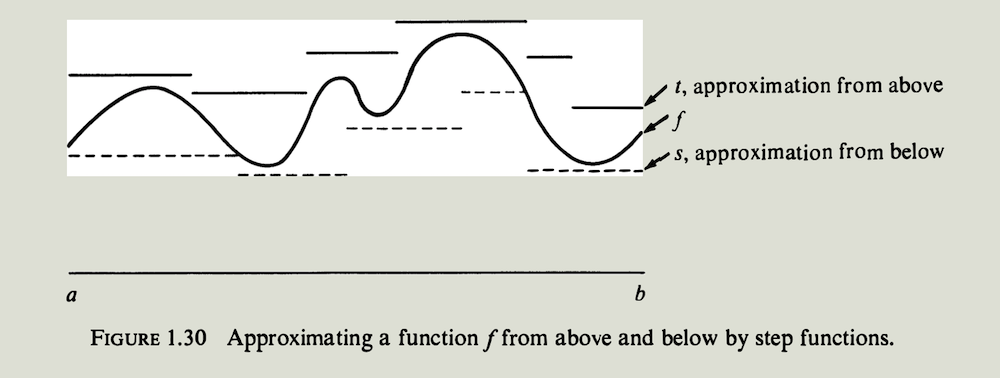
这个定义方法某种程度上是在模仿之前基础篇$I 1.3$提到的阿基米德穷竭法. 简单来说它的思想是这样的:用阶梯函数从下面和从上面逼近函数$f$ (如图$1.30$ 所示). 也就是说,我们选择任意一个图形位于$f$下方的阶梯函数$s$,再选择任意一个图形位于$f$上方的阶梯函数$t$. 然后考虑当选择所有可能的$s$和$t$时, 积分$\int_a^b s(x)\ dx$ 和 $\int_a^b t(x)\ dx$ 所有取值的集合. 因为$s(x) < t(x)$,由阶梯函数的比较定理$1.5$,我们有
\[\int_a^b s(x)\ dx < \int_a^b t(x)\ dx\]如果$f$的积分也具有比较定理的性质,因为$s(x)<f(x)<t(x)$,那么对于任意一对近似函数$s$和$t$, $f$的积分必定是落在积分$\int_a^b s(x)\ dx$ 和 $\int_a^b t(x)\ dx$ 之间的一个数. 如果有且仅有一个数满足这个性质,我们就把$f$的积分定义为这个数.
这个定义过程唯一的麻烦出现在第一步. 不幸的是,不是每一个函数都能用阶梯函数从上和从下近似. 例如,由
\[f(x) = \dfrac{1}{x}\ (x \ne 0),\quad f(0)= 0\]这组等式给出的函数对所有实数都有定义,但在任何包含原点的区间$[a,b]$ 上,我们无法用阶梯函数围住$f$. 这是因为$f$ 在原点附近能取得任意大的值,换句话说,在原点的每个领域内$f$是无界的 (见图$1.31$). 因此,我们需要把定义的对象限制在那些在$[a,b]$ 上有界的函数上,即对于这种函数$f$,存在一个数$M>0$,使得对$[a,b]$ 内的每个$x$ 都有
\[-M \le f(x) \le M \tag{1.5}\]从几何上看,这样一个函数的图形位于两个取值分别为$-M$和$M$的常值阶梯函数$s$和$t$的图形之间. (见图$1.32$)

我们说$f$以$M$为界 ($f$ is bounded by $M$). $(1.5)$中两个不等式也可以写成:
\[|\ f(x)\ | \le M\]解决了这一点麻烦,我们就可以开始定义一般函数的积分.
有界函数积分的定义 令$f$为定义在$[a,b]$上的有界函数,令$s$和$t$是定义在$[a,b]$上使得
\[s(x) \le f(x) \le t(x) \tag{1.6}\]对所有$x$都成立的任意阶梯函数. 如果对每一对满足不等式$(1.6)$ 的阶梯函数$s$和$t$,有且仅有一个数$I$ 使得
\[\int_a^b s(x)\ dx \le I \le \int_a^b t(x)\ dx \tag{1.7}\]那么这个数$I$称为函数$f$从$a$到$b$ 的积分,记为$\int_a^b f(x)\ dx$ 或 $\int_a^b f $ . 当这样一个$I$ 存在时,我们说函数$f$在$[a.b]$上是可积的(integrable). 函数$f$称为被积函数 (integrand) , 数$a$和$b$ 称为积分限 (limits of integration),区间$[a,b]$ 称为积分区间 (interval of integration).
当$f$在$[a,b]$ 上可积时,如果$a<b$,我们定义$\int_b^a f(x)\ dx = - \int_a^b f(x)\ dx$ . 我们也定义$\int_a^a f(x) = 0$ .
1.17 上积分和下积分
假设$f$在$[a,b]$ 上有界,如果$s$和$t$是满足不等式$(1.6)$ 关系的阶梯函数,我们说$s$在$f$之下,$t$在$f$之上,写作$s\le f\le t$ .
令$S$ 表示当$s$取遍$f$之下所有阶梯函数时得到的所有数$\int_a^b s(x)dx$ 组成的集合. 令$T$表示当$t$取遍$f$之上所有阶梯函数时得到的所有数$\int_a^b t(x)dx$ 的集合. 也就说,令
\[S = \left\{ \int_a^b s(x)\ dx\ \bigg| s \le f \right\},\quad T=\left\{ \int_a^b t(x)\ dx\ \bigg| f \le t\right\}\]显然$S$和$T$都是非空实数集 (因为$f$是有界的) . 而且由于$s \le f \le t$ 有 $\int_a^b s(x)\ dx \le \int_a^b t(x)\ dx $ (阶梯函数性质之比较定理),即 $S$ 中的每个数都小于等于$T$ 中的每个数. 根据 上确界和下确界的基本性质之定理I.34 ,$S$有一个上确界,$T$有一个下确界,且对所有满足$s\le f \le t$ 的阶梯函数$s$和$t$ ,有不等式
\[\int_a^b s(x)\ dx \le \sup S \le \inf T \le \int_a^b t(x)\ dx\]成立. 这说明$\sup S$和$\inf T$都满足作为$f$的积分定义的不等式$(1.7)$ . 因此,$f$在$[a,b]$上可积当且仅当$\sup S = \inf T$. 此时我们有
\[\int_a^b f(x)\ dx = \sup S = \inf T\]数 $\sup S$ 称为$f$的下积分,记为$\mathit{\underline{I}}(f)$. 数 $\inf T $ 称为$f$的上积分,记为$\bar{I}(f)$. 于是我们有
\[\mathit{\underline{I}}(f) = \sup \left\{ \int_a^b s(x)\ dx\ \bigg| s \le f \right\}\ , \quad \bar{I}(f) = \inf \left\{ \int_a^b t(x)\ dx\ \bigg| f \le t \right\}\]上述论证也证明了以下定理:
定理 1.9 每个在$[a,b]$上有界的函数$f$ 都有一个下积分$\mathit{\underline{I}}(f)$ 和一个上积分$\bar{I}(f)$ , 对所有满足$s\le f \le t$ 的阶梯函数$s$和$t$ , 有不等式
\[\int_a^b s(x)\ dx \le \mathit{\underline{I}}(f) \le \bar{I}(f) \le \int_a^b t(x)\ dx\]成立. 函数$f$在$[a,b]$上可积当且仅当它的上积分和下积分相等,此时我们有
\[\int_a^b f(x)\ dx = \mathit{\underline{I}}(f) = \bar{I}(f)\]1.18 把纵标集的面积表示为一个积分
在1.6 节中,我们把面积的概念公理化定义为具备某些性质的一个集合函数. 基于这些性质,我们把非负阶梯函数的积分定义为它的纵标集的面积 (见1.12节). 现在我们来证明任何可积的非负函数的积分也等于纵标集的面积。回忆一下,区间$[a,b]$上的非负函数$f$的纵标集是所有满足不等式$a \le x \le b,\ 0\le y \le f(x)$ 的点$(x,y)$ 的集合.
定理1.10 令 $f$ 是一个在$[a,b]$ 上可积的非负函数,令$Q$表示$f$在$[a,b]$上的纵标集,则$Q$是可测的且面积等于积分$\int_a^b f(x)\ dx$ .
证明: 令$S$和$T$是满足 $S \subseteq Q \subseteq T$ 的两个阶梯区域. 由阶梯函数积分的定义,则有在$[a,b]$上满足 $s \le f \le t$ 的两个阶梯函数$s$和$t$,使得
\[a(S) = \int_a^b s(x)\ dx \ ,\quad a(T) = \int_a^b t(x)\ dx\]因为$f$在$[a,b]$ 上可积,由有界函数积分的定义,对所有满足$s\le f \le t$ 的阶梯函数$s$和$t$ ,$I = \int_a^b f(x)\ dx$ 是使不等式
\[\int_a^b s(x)\ dx \le I \le \int_a^b t(x)\ dx\]成立的唯一的数。即对于满足$S\subseteq Q \subseteq T$ 的所有阶梯区域$S$和$T$ , $I$也是满足$a(S) \le I \le a(T)$ 的唯一的数. 根据面积公理中的穷竭性,$Q$是可测的,且$a(Q) = I = \int_a^b f(x)\ dx$. $#$
令$Q$表示定理$1.10$中$f$的纵标集,令$Q’$ 表示从$Q$中移去$f$图形上的点后所得到的点集, 也就是说,令
\[Q' = \left\{ (x,y)\ \big| a \le x \le b,\ 0 \le y \lt f(x) \right\}\]类似地按定理$1.10$中的论证也能证明$Q’$是可测的且$a(Q’) = I = a(Q)$. 证明过程如下.
证明: 因为$f$在$[a,b]$ 上可积,由有界函数积分的定义,对所有满足$s\le f \le t$ 的阶梯函数$s$和$t$ ,$I = \int_a^b f(x)\ dx$ 是使不等式
\[\int_a^b s(x)\ dx \le I \le \int_a^b t(x)\ dx\]成立的唯一的数.
对于满足 $S’\subseteq Q’\subseteq T’ $ 的任意一对阶梯区域$S’$和$T’$ ,因为$Q’$不包含$f$上的点, $S’$和$T’$对应的阶梯函数是所有满足$s’ \lt f \le t’$ 的阶梯函数. 由前面论证可知至少存在一个数$I=\int_a^bf(x)dx$ 使得不等式
\[\int_a^b s’(x)\ dx \le I \le \int_a^b t'(x)\ dx\]对于所有满足$s’\lt f \le t’$的$s’$和$t’$都成立.
假设存在另一个数$I’ \ne I$ 使$\int_a^b s’(x)\ dx \le I’ \le \int_a^b t’(x)\ dx$成立,当$t’(x)=f$时,若$I’>I$则不等式不可能成立,所以只可能$I’< I$. 此时必存在一个$s’ < f$ 使得$I’ \lt \int_a^b s’(x)dx < I$,则不等式也无法成立,所以假设不成立, 即$I$也是使不等式$\int_a^b s’(x)\ dx \le I \le \int_a^b t’(x)\ dx$ 成立的唯一的数. 由阶梯函数积分的定义有:
\[\int_a^b s'(x)\ dx = a(S')\ ,\quad \int_a^b t'(x)\ dx = a(T')\]则$I$是使$a(S’) \le I \le a(T’)$ 成立的唯一的数.
根据面积公理中的穷竭性,$Q’$是可测的,且$a(Q’) = I = \int_a^b f(x)\ dx= a(Q)$. $#$
再根据面积公理中的可减性 (Difference property) ,点集$Q-Q’$ 是可测的,且有 $a(Q-Q’)= a(Q)-a(Q’) = 0$. 从而我们证明了以下定理:
定理1.11 令$f$是一个在$[a,b]$上可积的非负函数,则$f$的图形即点集
\[\left\{\ (x,y)\ \big| \ a \le x \le b,\ y = f(x) \ \right\}\]是可测的,且面积等于0.
1.19 积分理论和积分技巧的非正式评注
在这个阶段出现了两个基本问题:$(1)$ 哪些有界函数是可积的? $(2)$ 给定一个可积函数$f$, 如何计算$f$的积分?
关于问题$(1)$ , 注意有界函数不一定是可积的. 反例:狄利克雷函数 (Dirichlet function)
\[D(x)= \left\{ \begin{array}{} \hspace{-1.5em} 1 \ ,\quad x \in \mathbb{Q} \\ \hspace{0.5em} 0 \ ,\quad x \in \mathbb{R}-\mathbb{Q} \\ \end{array} \right.\]在有理数点和无理数点对应的函数值不相等,根据积分的定义无法在划分的区间$\Delta x$ 内找到一个确定的高度,也就无法得到一个矩形来计算出面积, 所以狄利克雷函数是黎曼不可积的.
第一个问题属于“积分理论”的范畴,而第二个问题属于“积分技巧的范畴”. 问题$(1)$的完整回答超出了入门课程的范围,本书将不会给出. 我们将只给出仅需基本概念就能理解的部分回答.
首先我们介绍一类重要的函数,称为单调函数 (monotonic functions). 下一节我们会定义这类函数并给出一些例子. 然后我们将证明所有单调有界函数都是可积的. 幸运的是,实践中出现的大部分函数都是单调函数或单调函数的和,因此这个小范围的积分理论的结论的应用是相当广泛的.
“积分技巧”的讨论从$1.23$节开始,我们将计算$p$为正整数时的积分$\int_a^b x^p\ dx$. 然后我们将从积分的定义导出积分的一般性质,例如线性性和可加性, 并说明这些性质如何帮助我们扩展关于特殊函数的积分的知识.
