1.12 阶梯函数积分的定义
本节我们介绍阶梯函数的积分. 构造出的定义将使得非负阶梯函数的积分与它的纵标集的面积相等.
令$s$是定义在$[a,b]$上的阶梯函数,令$P={x_0, x_1,\cdots x_{n-1},x_n}$ 是$[a,b]$的一个划分,使得$s$在$[a,b]$的每个开子区间上都为常数,把$s$在第$k$个开子区间上取得的常值记为$s_k$ , 从而有
\[s(x) = s_k \quad 当\ x_{k-1} < x < x_k,\ k=1,2,\cdots n\]阶梯函数积分的定义 $s$的从$a$到$b$的积分,用符号$\int_{a}^{b}s(x)\ dx$ 表示, 由以下公式定义:
\[\int_{a}^b s(x)\ dx = \sum_{k=1}^n s_k \cdot (x_k-x_{k-1}) \tag{1.3}\]也就是说,为了计算此积分,我们用第$k$个子区间的长度乘上常值$s_k$ ,然后把这些乘积加起来.
注意$s$在分点处的取值是无关紧要的 (immaterial),因为它们不在定义式 $(1.3)$ 中出现. 特别地,如果$s$在开区间$(a,b)$上 都是一个常数,比方说 $s(x) = c \ (a < x <b)$ ,那么我们有
\[\int_a^b s(x) \ dx = c \sum_{k=1}^n (x_k-x_{k-1}) = c (b-a)\]积分与端点处的函数值$s(a)$ 和 $s(b)$ 无关. 如果 $c > 0$ 且对闭区间$[a,b]$上所有$x$都有$s(x) = c$ ,则$s$的纵标集是一个底边长$b-a$ 高为$c$ 的矩形. $s$的积分是$c(b-a)$,即这个矩形的面积. 改变$s$在端点$a$或$b$处的值只是改变了$s$的纵标集,但不会改变$s$的积分或纵标集的面积. 例如,图$1.22$ 展示的两个纵标集具有相同的面积.
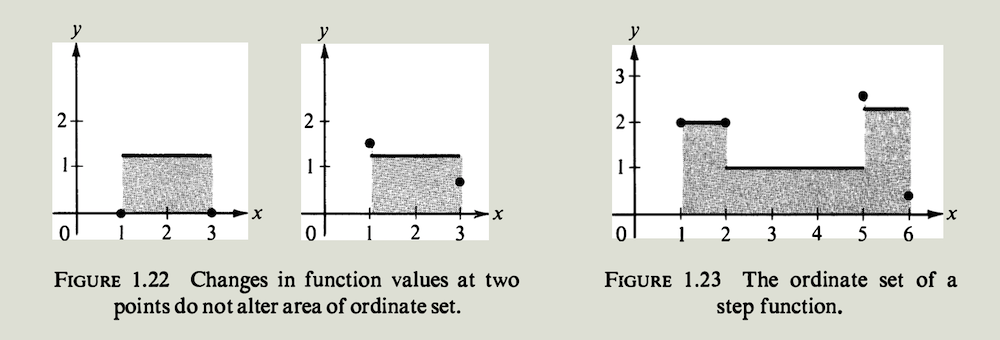
非负阶梯函数$s$的纵标集包含了有限个矩形,每个矩形在对应函数值为常数的区间上;阶梯函数的纵标集可能包含或缺少某些垂直线段,取决于$s$在分点处如何定义. $s$的积分等于各个矩形的面积之和,与$s$在分点处的取值无关. 这与面积公理定义的事实是一致的:垂直线段的面积为$0$,对纵标集的面积没有影响. 在图$1.23$中,阶梯函数$s$在开区间$(1,2)$ $(2,5)$ 和$(5,6)$ 分别取值为$2,1$和$\frac{9}{4}$,它的积分等于
\[\int_1^6 s(x)\ dx = 2 \cdot (2-1) + 1 \cdot (5-2) + \dfrac{9}{4} \cdot (6-5) = \dfrac{29}{4}\]必须注意,只要$s$在划分$P$ 的开子区间上都是常数, $(1.3)$中的积分公式的结果就与$P$ 的选择无关. 例如,通过插入一个新的分点$t$, 其中$x_0 < t < x_1$,我们把$P$ 改为更精细的划分$P’$. 此时$(1.3)$ 右边的第一项被替换为$s_1 \cdot (t-x_0)$ 和 $s_1 \cdot(x_1-t)$ ,其余项保持不变. 因为
\[s_1 \cdot (t-x_0) + s_1 \cdot (x_1 -t) = s_1 \cdot (x_1 - x_0)\]整个和的值是不变的. 我们可以通过每次插入一个新的分点,把划分从$P$ 改为任意更精细的划分$P’$,因为每次插入后积分定义式$(1.3)$ 的和都会保持不变,所以对所有$P$的精细划分,积分都是相同的.
1.13 阶梯函数积分的性质
本节我们来描述阶梯函数积分的若干基本性质。大部分性质在用几何解释时都是显然的,有些甚至是平凡 (trivial) 的. 所有这些性质都可以推广到更一般函数的积分,并且一旦确立了阶梯函数的这些性质,证明它们在一般情况下也成立就是简单的事了。下面把这些性质作为定理列出来,并且对阶梯函数积分每种性质的几何解释是根据面积给出的. 定理的解析证明在$1.15$节作为习题.
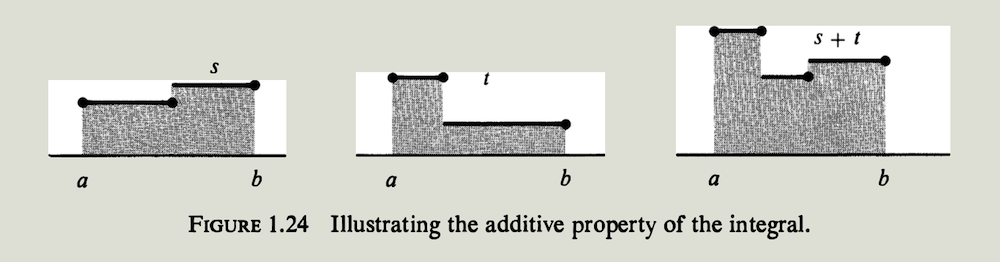
第一个性质指出,两个阶梯函数之和的积分等于积分的和. 这称为可加性,在图$1.24$中说明.
定理1.2 可加性 (ADDITIVE PROPERTY)
\(\int_a^b [s(x) +t(x)]\ dx= \int_a^b s(x)\ dx + \int_a^b t(x)\ dx\)
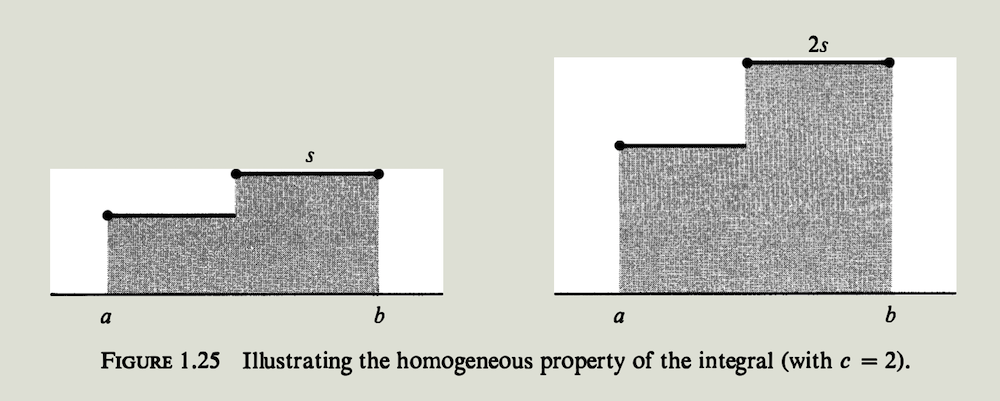
下一个性质是齐次性 (又称比例性,倍乘性), 见图$1.25$. 它指出如果阶梯函数值 (作为积分函数的自变量) 乘以$c$倍,则整个积分的结果也会变为原来的$c$倍 (放缩相同的比例).
定理1.3 齐次性 (HOMOGENEOUS PROPERTY) 对任意实数$c$ ,我们有
\[\int_a^b c \cdot s(x)\ dx = c\int_a^b s(x)\ dx\]可加性和齐次性组合在一块就是“线性”的性质.
定理1.4 线性性质 (LINEARITY PROPERTY) 对任意实数$c_1$和$c_2$ ,我们有
\[\int_a^b [c_1 \cdot s(x) + c_2 \cdot t(x)]\ dx = c_1 \int_a^b s(x)\ dx + c_2 \int_a^b t(x)\ dx\]接下来我们有一个比较定理,它告诉我们如果在整个$[a,b]$上一个阶梯函数的值都比另一个大,则在这个区间上它的积分也较大.
定理1.5 比较定理 (COMPARISON THEOREM) 如果对$[a,b]$内的每个$x$ 都有 $s(x) < t(x)$ , 则
\[\int_a^b s(x)\ dx < \int_a^b t(x)\ dx\]从几何上解释,这个定理反映了面积函数的单调性. 如果一个非负阶梯函数的纵标集位于另一个之内,则较小区域的面积小于较大区域的面积.
前面的性质涉及到的都是定义在同一区间上的阶梯函数积分,积分还具有把不同区间上的积分联系起来的重要性质,其中的性质我们列为以下定理.
定理1.6 关于积分区间的可加性 (ADDITIVITY WITH RESPECT TO THE INTERVAL OF INTEGRATION)
\[\int_a^c s(x)\ dx + \int_c^b s(x)\ dx = \int_a^b s(x)\ dx \quad其中\ a < c <b\]这个定理反映了面积的可加性,见图$1.26$. 如果一个纵标集被分解成两个纵标集,则两部分面积之和等于整个面积.

下一个定理可描述为平移不变性. 如果一个阶梯函数$s$ 被“移动”了距离$c$,得到是另一个纵标集的阶梯函数$t$,通过等式$t(x)=s(x-c) $ 与$s$联系起来. 如果$s$是定义在$[a,b]$上,则$t$定义在$[a+c,b+c]$ 上,且它们的纵标集是全等的,具有相同的面积. 这个性质的解析表示如下:
定理1.7 平移不变性 (INVARIANCE UNDER TRANSLATION)
\[\int_a^b s(x)\ dx = \int_{a+c}^{b+c} s(x-c)\ dx \quad 对任意实数c都成立\]当$c>0$时,定理的几何意义见图$1.27$. 当$c<0$时,函数的纵标集会向左移动.
齐次性 (定理$1.3$) 解释了当在$y$轴上尺度改变 (放缩被积函数值)时,积分会发生什么变化. 下述定理描述的是$x$轴上尺度改变时的情况. 如果$s$是定义在$[a,b]$上的阶梯函数,我们用一个因子$k>0$乘以所有$x$坐标来扭曲水平方向上的尺度,则新图形是定义在区间$[ka,kb]$上的阶梯函数$t$,通过等式
\[t(x) = s(\dfrac{x}{k}) \quad ka \le x \le kb\]联系起来.如图$1.28$ 所示是$k=2$时的例子,尺度改变后的图形面积是原图形的2倍. 更一般地,用正因子$k$改变水平方向上的尺度,效果相当于用 $k$ 乘以原积分. 这个性质可用以下形式解析表示:
定理 1.8 积分区间的扩大或缩小 (EXPANSION OR CONTRACTION OF THE INTERVAL OF INTEGRATION)
\[\int_{ka}^{kb} s(\dfrac{x}{k})\ dx = k \int_a^b s(x)\ dx \quad 对任意 k > 0 成立\]
直到现在,当我们使用符号$\int_a^b$ 时都默认下限$a$ 是小于上限$b$ ,为了进一步扩展符号的适用范围,考虑下限大于上限的积分,我们可以定义
\[\int_b^a s(x)\ dx = - \int_a^b s(x)\ dx \quad 其中\ a < b\ \tag{1.4}\]我们还定义
\[\int_a^a s(x)\ dx = 0\]这是令$(1.4)$式中$a=b$ 得出的定义. 这些约定使得定理$1.6$ (积分区间的可加性) 不仅当$c$在$a$和$b$之间时成立,而且对$a,b,c$ 的任意排列都成立,定理$1.6$有时可以写成如下形式:
\[\int_a^c s(x)\ dx + \int_c^b s(x)\ dx + \int_b^a s(x)\ dx = 0\]类似地,我们可以扩展定理$1.8$ 的有效范围,允许常数$k$为负数. 特别地,当$k=-1$,由定理$1.8$和定义$(1.4)$ 有
\[\int_a^b s(x)\ dx = \int_{-b}^{-a} s(-x)\ dx\]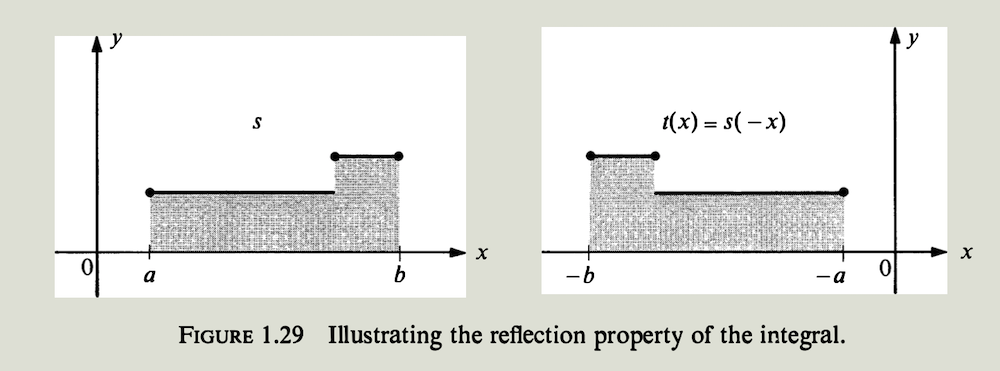
我们把这一性质称为积分的反射性 (reflection property),因为函数$t$ 的图形是通过$y$轴反射$s$的图形得到的,由关系式$t(x)=s(-x)$ 给出. 见图$1.29$的例子.
1.14 积分的其他记号
符号$\int_a^b s(x)\ dx$ 中的字母$x$ 在定义中不起本质作用,用任何其他字母都可以. 字母$t, u, v,z$ 也很常用. 这就是说可以用$\int_a^b s(t)\ dt$ ,$\int_a^b s(u)\ du$ 等等替代$\int_a^b s(x)\ dx$ . 这些都是表示同一事物的可选记号. 这样使用的符号$x, t, u$等被称为“哑变量”,类似于求和记号中的哑指标.
一些微积分教科书的作者倾向于把哑变量和符号$\mathrm{d}$一起省略,而简单地把积分写作$\int_a^b s$. 使用这个缩写的充分理由在于它着重强调了积分只依赖函数$s$ 和区间$[a,b]$ ,而且缩写会让某些公式看起来更简单,例如可加性的公式变为$\int_a^b (s+t) = \int_a^b s + \int_a^b t$. 另一方面,缩写不适用于定理$1.7$和定理$1.8$ 这样的公式。 更重要的是,我们后面将发现莱布尼兹记号具有某些实用的优点,在这个阶段似乎多余的符号$dx$ , 在许多涉及积分的常规计算中,却是极有用的计算工具.
