1.6 把面积的概念定义为集合函数
从纯数学的角度看,当我们给平面区域指定一个非负实数作为面积,我们就有了一个面积函数$a$, 因为平面区域是点的集合, 面积函数的自变量是集合 (点集$S$),定义域就是集合的集合 (所有可计算面积的点集的集合),函数值就是实数$a(S)$. 像这样,定义域是集合的集合 (collection of sets)且函数值是实数的函数,称为集合函数 (set function).
一个基本问题是:给定平面点集$S$,我们应该赋予$S$的面积函数值$a(S)$是多少? 我们的解决方法是从面积应该具备的性质出发,把这些性质作为公理。任何满足这些公理的集合函数都被称为面积函数。注意不是所有平面点集都有面积函数,为了理论的严谨性,应该先证明面积函数的存在性。这里我们不展开证明,而是假定面积函数存在,由公理直接推导出它的性质。关于面积函数的基本构造,可以参考《高观点下的初等几何》的第14章和第22章。 (Edwin E. Moise, Elementary Geometry From An Advanced Standpoint, Addison Wesley Publishing Co., 1963.)
那些可以计算面积的集合叫作可测集 (measurable sets). 所有可测集的集合记为$\mathscr{M}$ . 面积公理包含了关于可测集的足够信息,使我们能证明微积分应用中出现的几何图形都属于$\mathscr{M}$, 这些图形的面积都可以用积分来计算。
公理5指出每个矩形都是可测的,且面积是边长的乘积. “矩形”指的是任何与平面点集 \(\{(x,y)\ |\ 0 \le x \le h,\ 0 \le y \le k\}\) 全等的集合 (这里全等与欧氏几何中的三角形全等的含义相同),其中$h \ge 0,\ k \ge 0$. 数$h$和$k$称为矩形的边长. 线段或点都可看作是矩形的特例 ( $h$或$k$至少有一个为$0$ ).
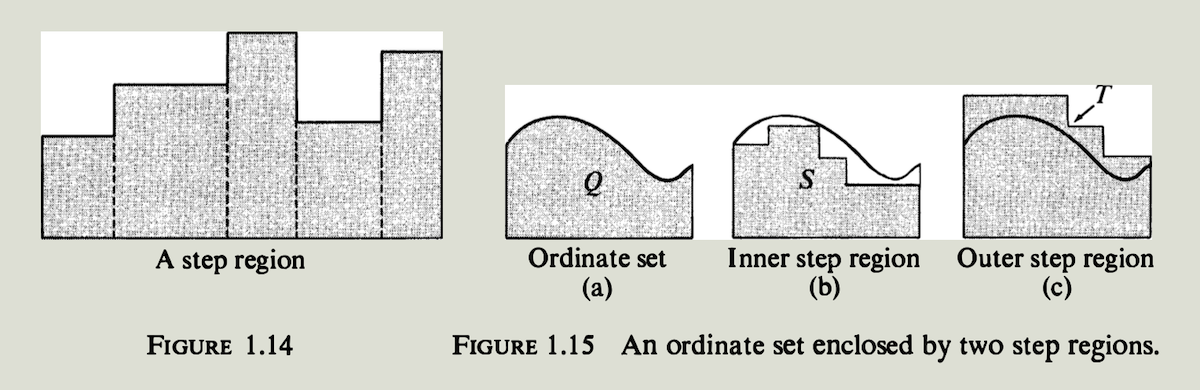
由矩形我们可以构建更复杂的集合. 图$1.14$ 中的集合是底边在$x$轴上的相邻矩形的有限并集, 称为阶梯区域 (step region). 由面积公理可推出每个阶梯区域都是可测的,而且它的面积是矩形块面积之和.
图$1.15(a)$ 是纵标集 (ordinate set) 的一个例子. 它的上边界是一个非负函数的图形. 公理6使我们能够证明许多纵标集是可测的,且可以通过内阶梯区域和外阶梯区域来逼近这样的点集并计算出面积, 如图$1.15(b)$和$(c)$所示.
下面给出作为公理的面积的定义 (Axiomatic definition of area). 正是这些公理使得我们可以用积分计算面积.
面积的公理化定义 假设平面中存在可测集的集合$\mathscr{M}$ 和一个以$\mathscr{M}$为定义域的集合函数$a$ 满足以下性质:
1. 非负性 (Nonnegative property) 对$\mathscr{M}$中的每个点集,我们有$a(S) \ge 0$.
2. 可加性 (Additive property) 如果$S$和$T$在$\mathscr{M}$ 中,则$S \cup T$ 和 $S \cap T$ 也在$\mathscr{M}$中. 且有
\[a(S\cup T) = a(S) + a(T) - a(S \cap T)\]3.可减性 (Difference property) 如果$S$和$T$都在$\mathscr{M}$中且$S \subseteq T$,则它们的差集$T-S$ 也在$\mathscr{M}$中. 且有
\[a(T-S) = a(T) - a(S)\]4.全等不变性 (Invariance under congruence) 如果集合$S$ 在$\mathscr{M}$中,且$T$与$S$全等,则$T$也在$\mathscr{M}$中,且有
\[a(S)=a(T)\]5.尺度的选择 (Choice of scale) 每个矩形$R$都属于$\mathscr{M}$,如果矩形的边长分别为$h$和$k$,则$a(R)=hk$.
6.穷竭性 (Exhaustion property) 令$Q$是被围在阶梯区域$S$和$T$之间的点集,即 \(S \subseteq Q \subseteq T \tag{1.1}\) 如果有且仅有一个实数$c$使得不等关系 \(a(S) \le c \le a(T)\)
对所有满足$(1.1)$的阶梯区域$S$和$T$ 都成立,则$Q$是可测的,且$a(Q) = c$.
公理1只是指出平面可测集的面积是一个正数或者零. 公理2告诉我们当一个集合由两部分构成 (这两部分可以重叠),并集的面积是两部分面积之和减去交集的面积. 特别地,如果交集面积为零,则并集面积就是两部分面积之和.
公理3指出,如果我们从一个较大的可测集$T$中移除一个可测集$S$, 剩余部分$T-S$是可测的,且面积可用减法求得,即$a(T-S)=a(T)-a(S)$. 特别地,这个公理蕴含着空集 $\emptyset $ 是可测的,且面积为零 (当S = T时). 由公理1非负性有$a(T-S)\ge 0$,则公理3也蕴含着单调性 (monotone property):对$\mathscr{M}$中的集合$S$和$T$, 当$S \subseteq T$ 时, 有 \(a(S) \le a(T)\)
换句话说,如果一个集合是另一集合的一部分,则它的面积不能大于较大的集合。
公理4对具有相同大小和形状的点集赋予相同的面积. 如果没有公理5关于矩形面积的性质,对集合$\mathscr{M}$中的每个集合,简单地将面积函数定义为$a(S)=0$, 也能满足前4条公理,但就没有了实际意义,公理5赋予矩形非零面积,排除了这种trival的情况。阶梯区域是由有限个底边在$x$轴的相邻矩形组成的, 由面积的可加性 (公理2) 和矩形面积公式 (公理5) 可知,阶梯区域也是可测集,且它的面积等于组成它的矩形面积之和。公理6包含了古希腊的穷竭法思想,将可测集的种类从阶梯区域推广到更一般的区域. 公理描述的性质使我们可以从矩形面积出发,计算出形状更复杂的区域的面积.
1.8 区间与纵标集
在积分理论中,我们主要关注定义域为$x$轴上区间的实函数. 区分区间是否包含端点有时是很重要的. 我们引入以下定义对区间进行分类.
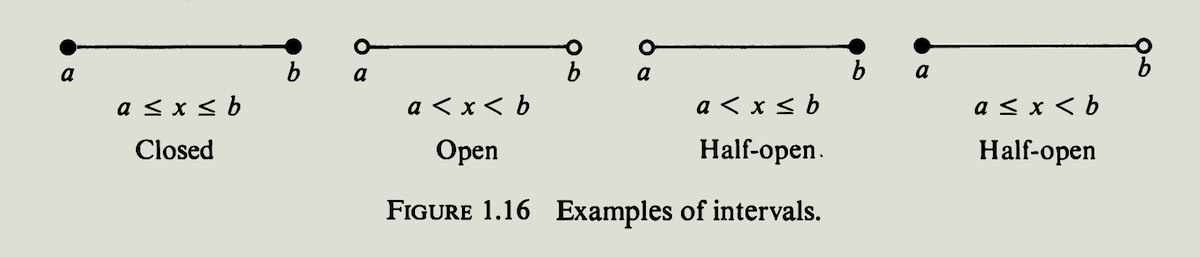
如果$a<b$,我们用$[a,b]$表示所有满足不等式 $a \le x \le b$ 的$x$的集合, 并把这个集合称为从$a$到$b$ 的闭区间 (closed interval). 对应的开区间记为$(a,b)$ ,是所有满足不等式 $a < x < b$ 的$x$的集合. 闭区间$[a,b]$包含端点$a$和$b$,而开区间不包括端点 (见图$1.16$). 开区间$(a,b)$也称为$[a,b]$的内部 (interior). 半开区间$(a,b]$和$[a,b)$只包括一个端点,分别由不等式$a < x \le b$ 和 $a \le x < b$ 定义.
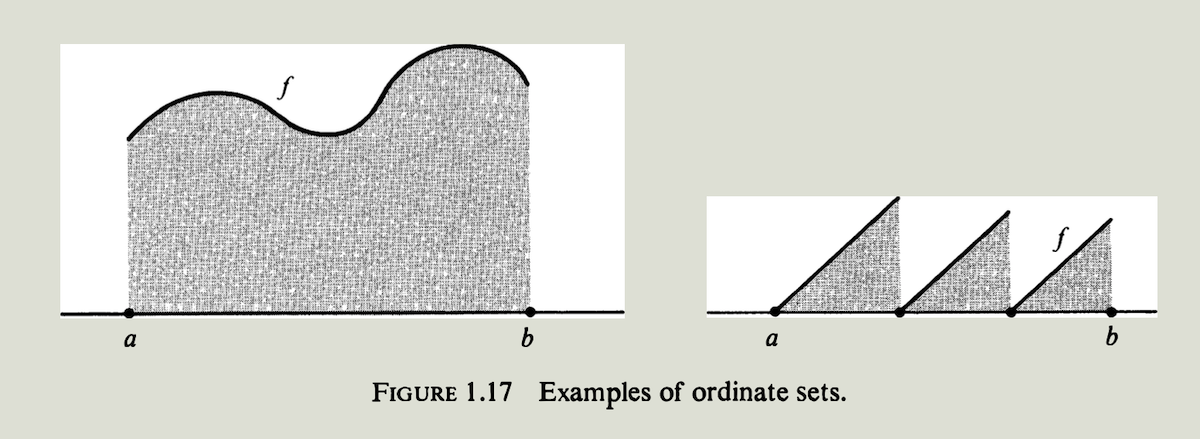
令$f$是一个非负函数,定义域是闭区间$[a,b]$. 平面上$f$的图形和$x$轴之间的部分叫做$f$的纵标集. 更确切地说,函数$f$的纵标集是所有满足不等式 \(a \le x \le b, \quad 0 \le y \le f(x)\) 的点$(x,y)$的集合. 图$1.17$ 例子中的阴影部分表示对应函数的纵标集.
纵标集是我们想要用积分方法求得其面积的几何对象. 我们会先为阶梯函数定义积分的概念,然后利用阶梯函数的积分来定义更一般函数的积分.
阶梯函数的积分理论极其简单,并且可以很自然地引出更一般函数的积分理论。为了定义阶梯函数的积分,首先必须给阶梯函数一个解析定义,这可以通过划分 (partition) 的概念给出。
1.9 划分与阶梯函数
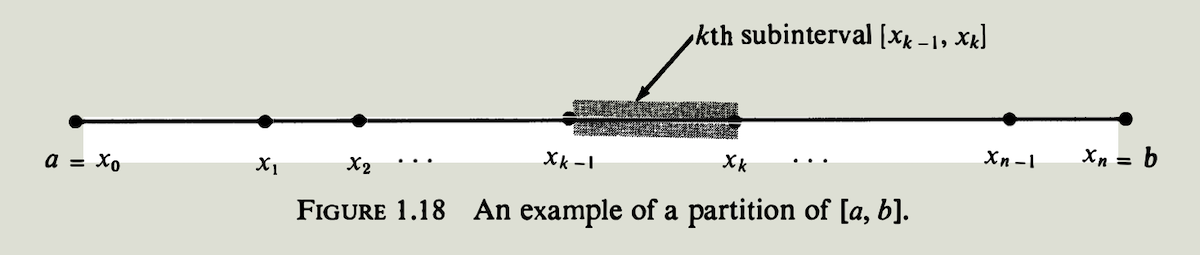
假设我们对一个给定的闭区间$[a,b]$插入$n-1$个分点,比方说$x_1,x_2,\cdots,x_{n-1}$,把闭区间分成$n$个子区间,分点只须满足 \(a < x_1 < x_2 < \cdots < x_{n-1} < b \tag{1.2}\) 为了方便起见, 我们用$x_0$表示端点$a$,用$x_n$表示端点$b$. 满足$(1.2)$ 的点的集合叫做$[a,b]$的划分$P$. 我们用符号 \(P = \{x_0, x_1,\cdots,x_n\}\) 来指明这个划分. 划分$P$确定了$n$个闭子区间 (closed subintervals):
\([x_0, x_1],[x_1,x_2],\cdots,[x_{n-1},x_n]\) 一个典型(typical) 的闭子区间是$[x_{k-1},x_k]$,称为划分$P$ 的第$k$个闭子区间, 如图$1.18$ 所示. 对应的开区间$(x_{k-1},x_k)$ 称为划分$P$的第$k$个开子区间.
现在我们来阐述阶梯函数的解析定义.
阶梯函数的定义 一个函数$s$的定义域是闭区间$[a,b]$ , 如果有一个$[a,b]$的划分$P={x_0,x_1,\cdots,x_n}$, 使得在$P$的每个开子区间上$s$的值都为常数,则函数$s$叫做阶梯函数. 也就是说,对每个$k=1,2,\cdots,n$,都有一个实数$s_k$, 使得 \(s(x) = s_k \quad(x_{k-1} < x < x_k)\) 阶梯函数有时被称为分段常值函数 (piecewise constant function).
注:在每个子区间的端点$x_{k-1}$和$x_k$ 函数必须有定义,但函数值不一定要等于$s_k$.
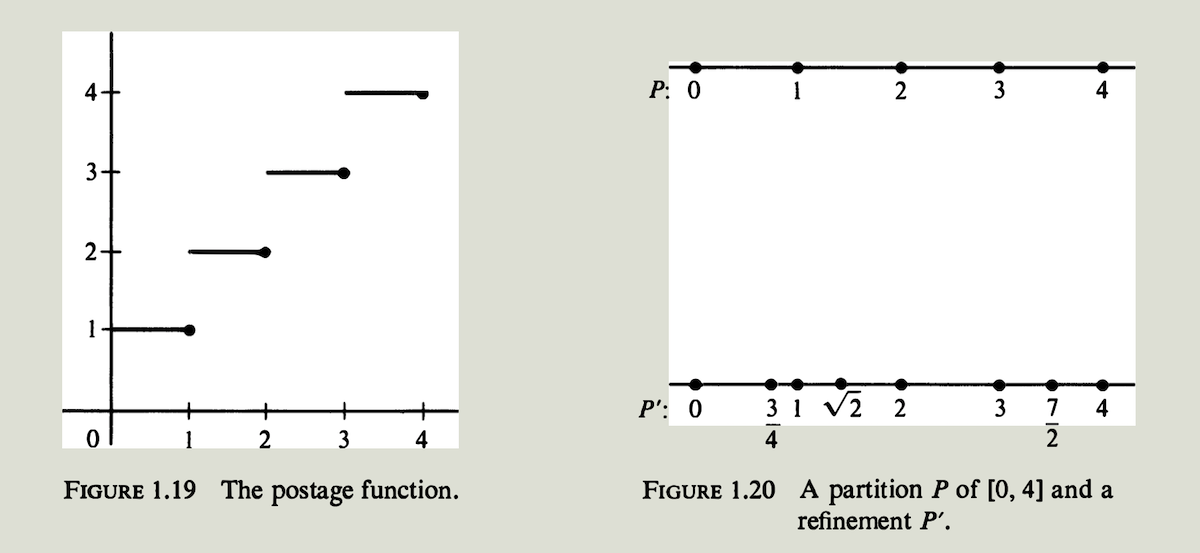
例子 阶梯函数一个熟悉的例子是“邮费函数” (postage function),见图$1.19$. 假设包裹重量在20磅以内的第一类邮件的费用是每盎司5美分,不足1盎司的部分按1盎司计费. 图$1.19$的部分图形展示了4盎司以内的邮件所需5美分邮票的数量,图形上的线段是包含右端点的半开区间. 20磅以内邮费函数的定义域是$[0,320]$. (1 pound = 16 ounces)
给定一个$[a,b]$的划分$P$,我们总能在已有分点的基础上加入 (adjoin) 更多的分点,从而形成一个新的划分. 这个新的划分$P’$叫做$P$的精细划分 (refinement of $P$). 我们说划分$P’$比$P$更精细. 例如,$P={0,1,2,3,4}$ 是区间$[0,4]$的一个划分,如果我们加入点$\dfrac{3}{4}, \sqrt{2}, \dfrac{7}{2}$ 就得到$[0,4]$的一个新的划分 $P’={0,\dfrac{3}{4},1,\sqrt{2},2,3,\dfrac{7}{2},4 }$. 这是$P$的一个精细划分 (见图$1.20$). 如果阶梯函数在$P$的开子区间上都是常数,那么它在$P$的每个精细划分$P’$的开子区间上也都是常数.
1.10 阶梯函数的和与积
把给定阶梯函数对应的函数值相加,可以构造新的阶梯函数。例如,假设$s$和$t$都是阶梯函数,两者都定义在同个区间$[a,b]$上. 令$P_1$和$P_2$是$[a,b]$的划分,$s$在$P_1$的每个开子区间上是常数,$t$在$P_2$的每个开子区间上是常数. 令$u=s+t$是通过等式 \(u(x) = s(x) + t(x) \quad (a \le x \le b)\) 定义的函数.
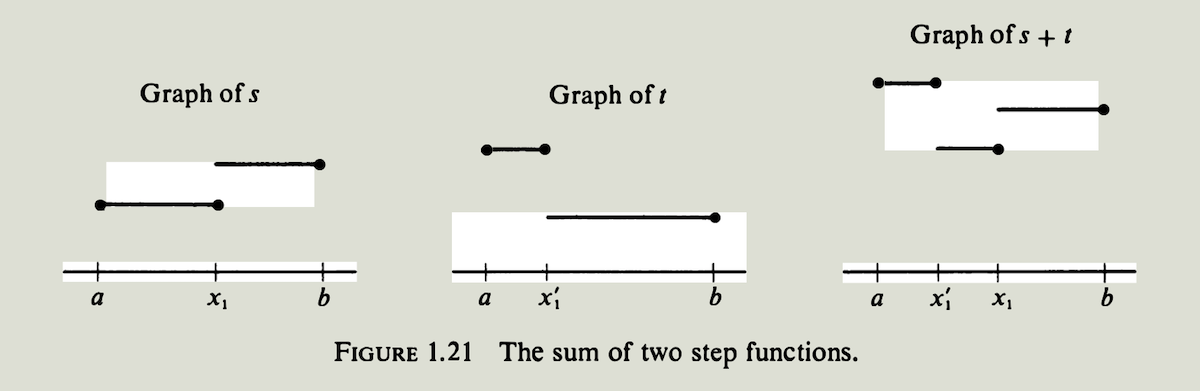
为了说明$u$实际上也是一个阶梯函数,我们需要展示(exhibit) 一个划分$P$, 使得$u$在$P$的开子区间上是常数。我们取$P_1$的所有点加上$P_2$的所有点,构造一个新的划分$P$, 这个划分是$P_1$和$P_2$的并集, 称为$P_1$和$P_2$的共同精细划分 (common refinement). 因为$s$和$t$在共同精细划分$P$的开子区间上都是常数,它们的函数值之和$u$也是常数. 见图 $1.21$的例子, $P_1={a,x_1,b}$,$P_2={a,x_1’,b}$,$P=P_1 \cup P_2={a,x_1’,x1,b}$.
类似地,两个阶梯函数之积 $v = s \cdot t$ 也是一个阶梯函数. 一个重要的特例是当其中一个函数为常数,比方说$t$在$[a.b]$上为常数,如果对$[a,b]$中的每个$x$都有$t(x)=c$,则每个函数值$v(x)$由常数$c$乘以阶梯函数$s(x)$得到.
1.11 习题
在这组习题中,$\lfloor x \rfloor$ 表示$\le x$的最大整数,称为最大整数函数,它的功能是向下取整,也称为下取整函数 (floor function).
$1.$ 对所有实数$x$,令$f(x)=\lfloor x \rfloor$,$g(x)=\lfloor 2x \rfloor$. 根据以下给定的公式,画出定义在区间$[-1,2]$上的函数$h$的图像.
$(a)$ $h(x)=f(x)+g(x)$
$(b)$ $h(x)=f(x)+g(\dfrac{x}{2})$
$( c )$ $h(x)=f(x)g(x)$
$(d)$ $h(x)=\dfrac{1}{4}f(2x)g(\dfrac{x}{2})$
$4.$ 证明下取整函数$\lfloor x \rfloor$ 的以下性质:
$\hspace{0.5em} (a)\quad \lfloor x+n \rfloor = \lfloor x \rfloor + n $ 对任意整数$n$都成立
\[(b)\quad \lfloor -x \rfloor = \left\{ \begin{array}{} -\lfloor x \rfloor & \mathrm{if} \ x \in \mathbb{Z} \\ -\lfloor x \rfloor - 1 & \mathrm{otherwise} \\ \end{array} \right. \hspace{25em}\] $\left(c\right)\quad \lfloor x+y \rfloor = \lfloor x \rfloor +\lfloor y \rfloor$ 或 $\lfloor x \rfloor + \lfloor y \rfloor + 1$
$ (d)\quad \lfloor 2x \rfloor = \lfloor x \rfloor + \lfloor x + \dfrac{1}{2} \rfloor $
$(e)\quad \lfloor 3x \rfloor = \lfloor x\rfloor + \lfloor x+\dfrac{1}{3}\rfloor + \lfloor x +\dfrac{2}{3} \rfloor$
(a) 证明: 令$\lfloor x+n \rfloor = m$ ,$m$为某个整数. 则有
\[\begin{align} m \le x+n < m+1 \hspace{-10.8em}\\ &\Longrightarrow m-n \le x < m-n+1 \\ &\Longrightarrow \lfloor x \rfloor = m-n \\ &\Longrightarrow \lfloor x \rfloor + n = m \end{align}\]因为我们已定义$\lfloor x+n \rfloor = m$,所以$\lfloor x+n \rfloor = \lfloor x \rfloor + n$ 对任意整数$n$都成立.
(b) 证明: 当$x \in \mathbb{Z}$ ,令$x = m$ ,$m$ 为某个整数. 则$\lfloor x \rfloor = m$. 由已知有
\[\begin{align} -x = - m \hspace{-7em}\\ &\Longrightarrow \lfloor -x \rfloor = -m \\ &\Longrightarrow \lfloor -x \rfloor = - \lfloor x \rfloor \quad\# \end{align}\]当$x \notin \mathbb{Z}$ ,令$\lfloor x \rfloor = m$,$m$为某个整数,则有
\[\begin{align} m < x < m+1 \quad (x \neq m \ 因为x \notin \mathbb{Z}) \hspace{-18em}\\ &\Longrightarrow -m - 1 < -x < -m \\ &\Longrightarrow \lfloor -x \rfloor = -m - 1 = - \lfloor x \rfloor -1 \quad\# \end{align}\](c) 证明: 令$\lfloor x \rfloor = m$ , $\lfloor y \rfloor = n$,$m,n$为某个整数,则有
$m \le x < m+1$ 和 $n \le y < n+1$. 两不等式相加有:
$m+n \le x+y < m+n+2$ . 所以$\lfloor x+y \rfloor$的取值只有两种可能:
$\lfloor x+y \rfloor = m+n$ 或 $\lfloor x+y \rfloor = m+n+1$ 即
$\lfloor x+y \rfloor = \lfloor x \rfloor + \lfloor y \rfloor $ 或 $\lfloor x+y \rfloor = \lfloor x \rfloor + \lfloor y \rfloor + 1$ $#$
