本章我们介绍积分的定义和积分的一些基本性质。为了理解定义我们必须先熟悉函数的概念。下面几节将专门解释函数的概念及其有关思想。
1.1 解析几何的基本概念
如前所述,积分的一个应用是面积的计算。通常我们不讨论面积本身,而是讨论某些东西的面积。我们有一些想要测量其面积的对象 (多边形区域,圆形区域,抛物线弓形等等). 如果我们希望得到不同类型对象的面积计算方法,我们首先必须找到一个有效的方法来描述这些对象。
正如古希腊人说做的那样,描述这些对象最原始的方法是绘制图形。笛卡尔(Rene Descartes, 1596-1650) 提出了一个更好的方法。他引进了解析几何学 (也称为笛卡尔几何)。笛卡尔的思想是用数表示几何点。表示出平面中的点的步骤如下:
选择两条垂直的参考线 (称为坐标轴),一条是水平的 (叫做$x$轴),一条是垂直的 (叫做$y$轴), 它们的交点用$0$表示,叫做原点。在$x$轴上$0$的右边选择一个方便的点,并将这个点与$0$的距离称为单位距离。沿着$y$轴的垂直距离通常用相同的单位距离来度量,尽管有时$y$轴使用不同的尺度更方便。平面 (有时称为$xy$平面) 内的每个点都被赋值一对数,称为坐标。这些数字告诉我们如何确定点的位置。图$1.1$说明了一些例子。坐标为$(3,2)$ 的点位于$y$轴右侧$3$个单位及$x$轴上方$2$个单位处。数字$3$ 被称为点的$x$坐标,数字$2$是点的$y$坐标。$y$轴左侧的点具有负的$x$坐标,$x$轴下方的点具有负的$y$坐标。一个点的$x$坐标有时称为横坐标 (abscissa),而$y$坐标称为纵坐标 (ordinate).
当我们写出一对数,例如$(a,b)$ 来表示一个点时,总是先写横坐标或$x$坐标$a$,因此$(a,b)$ 常被称为有序对. 显然两个有序对$(a,b)$和$(c,d)$表示同一个点当且仅当$a=c$且$b=d$. 如果$a$和$b$都是正的,则称点$(a,b)$在第一象限 (first quadrant); $a<0$且$b>0$ 的点则在第二象限;$a<0$且$b<0$的点在第三象限;$a>0$且$b<0$的点在第四象限. 图$1.1$在每个象限中展示了一个点。
表示空间中的点过程也是类似的。我们在空间中取三条互相垂直的直线交于一点 (作为原点). 这些直线确定三个互相垂直的平面. 空间中的每个点都可通过规定适当的符号来描述. 以后我们会更详细地讨论三维解析几何,目前我们仅关注平面解析几何。
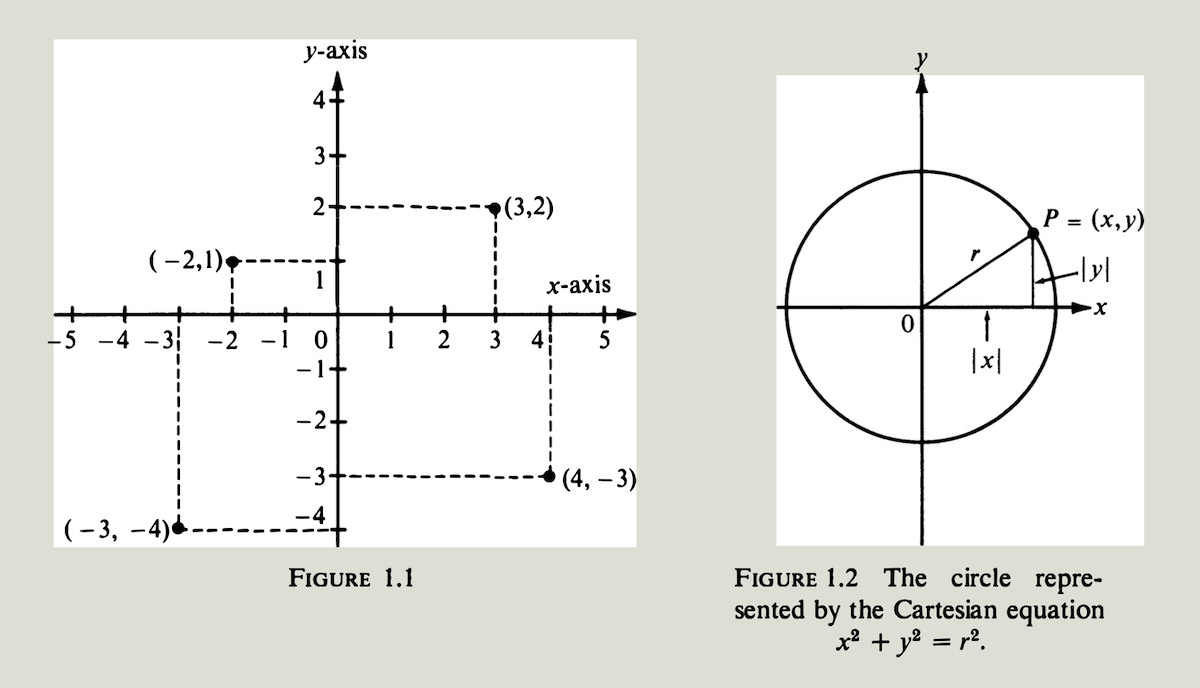
一个几何图形,例如平面上的一条曲线,是满足一个或多个特殊条件的点的集合。把这些条件转换成含有坐标$x$和$y$的表达式,我们就得到一个或多个表示图形特征的方程. 例如,考虑一个中心在原点,半径为$r$的圆,如图$1.2$所示。令$P$为圆上任意一点,设$P$的坐标为$(x,y)$,则线段$OP$是直角三角形的斜边,两条直角边的长度为$\lvert x\rvert$ 和 $\lvert y \rvert$ . 按照毕达哥拉斯(Pythagoras) 定理, 有:
\(x^2 + y^2 = r^2\) 这个方程称为圆的笛卡尔方程. 圆上的所有点满足方程,而其他点不满足。因此方程可以完整描述圆的特征。这个例子说明了怎样把关于点的几何语言简化成关于实数的解析语言。
微积分和解析几何在历史发展过程中紧密地交织在一起,一个学科中的新发现能带动另一个学科的进展,两个学科是放在一起研究的。本书也按照发展史的顺序来介绍微积分和解析几何,然而我们的主要目的是讨论微积分,相关的解析几何概念将在需要时加以讨论。实际上,只需少许基本的平面解析几何概念,就能理解微积分的基础知识。进一步拓展微积分的范围和应用需要对解析几何进行更深入的学习,后面我会利用向量方法以及微积分方法来研究它。至此之前,只需熟悉一点函数图形的绘制即可。
1.2 函数. 非正式描述与举例
人类探索的各个领域都涉及到某个对象的集合与另一个的对象集合之间的关系。图形、图表、曲线、表格、公式以及盖洛普民意调查 (Gallup polls) , 对每个读报的人来说都是熟悉的。这些仅仅是定量描述特殊关系的手段。数学家把某些类型的关系称为函数。我们在这一节给出函数概念的非正式描述。$1.3$节给出正式定义。
例1 使自然长度的钢弹簧伸长距离$x$所需要的力$F$ 与$x$成比例,也就是说$F=cx$ 其中$c$是一个与$x$无关的数,称为弹簧常数. 这个公式称为胡克定律 (Hooke’s Law),是十七世纪中叶Robert Hooke发现的.
例2 立方体的体积是它边长的函数。如果边长为$x$, 则体积$V$由公式$V = x^3$ 给出.
例3 素数是一个大于1的整数,它无法表示成$n=ab$ 的形式,其中$a$ 和 $b$ 都是小于 $n$ 的正整数。前几个素数是$2,3,5,7,11,13,17,19,23$. 给定实数$x>0$, 数出小于或等于$x$的素数的个数是可以做到的. 当$x$已知时,尽管找不到简单的代数公式来计算个数, 我们仍把这个数字称为$x$的函数.
“函数”这个词是由$Leibniz$ 引进数学的,他使用这一术语来特指某些类型的数学公式。后来人们意识到莱布尼兹的函数概念范围太局限,于是这个词的意义又经过了多个阶段的推广。今天,函数的含义基本上是这样的:给定两个集合$X$和$Y$, 函数是把$X$的每个元素关联到$Y$中的一个(且只有一个)元素的一种对应关系。集合$X$称为函数的定义域 (domain),集合$Y$中那些与$X$关联的元素集合称为函数的值域 (range) ,值域可以是$Y$的全部,也可以不是.
英文字母和希腊字母例如$f,g,h,F,G,H$和 $\varphi$ 常用来表示函数。如果$f$是一个给定的函数且$x$是定义域中的一个对象, 则$f(x)$ 用来指代值域中通过$f$与$x$ 关联的那个对象,$f(x)$被称为函数$f$在$x$处的值,或叫做$x$在$f$下的像 (image). 符号$f(x)$读作”$f$ of $x$”.
函数的概念可以用许多图解方式来说明. 例如,图$1.3(a)$中$X$和$Y$看成是点的集合,箭头用来表示$X$中一个点$x$ 与在$Y$中的像点$f(x)$ 的配对关系。另一种图解见图$1.3(b)$. 这里函数$f$ 被想象成一台机器,把集合$X$中的对象输入机器,则输出$Y$中的一个对象。当对象$x$输入机器时,输出的是对象$f(x)$.

尽管函数的概念对定义域和值域中对象的性质没有限制,但在初等微积分中我们主要研究定义域和值域都为实数集的那些函数,这样的函数被称为实变量的实值函数 (real-valued functions of a real variable),或者更简短地称为实函数 (real functions). 它们可以用$xy$平面上的图形来进行几何表示。我们把定义域$X$画在$x$轴上,在每个点$x$的上方,我们标出点$(x,y)$ , 其中$y=f(x)$. 点$(x,y)$ 的全体称为函数的图像 (graph of the function).
我们来看更多实函数的例子:
例4 恒等函数 假设对所有实数$x$, 都有$f(x)=x$,则称这个函数为恒等函数 (The identity function). 它的定义域是实直线,即所有实数的集合。对$f$图形上的每一点$(x,y)$都有$x=y$. 图像是与坐标轴成等角的一条直线 (见图$1.4$) , $f$的值域是所有实数的集合.
例5 绝对值函数 考虑这样一个函数,它对每个实数$x$赋值一个非负数 $\lvert x \rvert$ , 部分图像见图$1.5$. 用 $\varphi$ 表示这个函数,对所有实数$x$,我们有$\varphi(x) = x$. 例如,$\varphi(0)=0, \varphi(2)=2, \varphi(-3)=3$. 这里我们列出绝对值的若干性质,用函数记号表示.
\(\begin{align} &(a) \quad \varphi(-x) = \varphi(x) \\ &(b) \quad \varphi(x^2) = x^2 \\ &(c) \quad \varphi(x+y) \le \varphi(x) + \varphi(y) \quad (三角不等式) \\ &(d) \quad \varphi[\varphi(x)] = \varphi(x) \\ &(e) \quad \varphi(x) = \sqrt{x^2} \end{align}\)

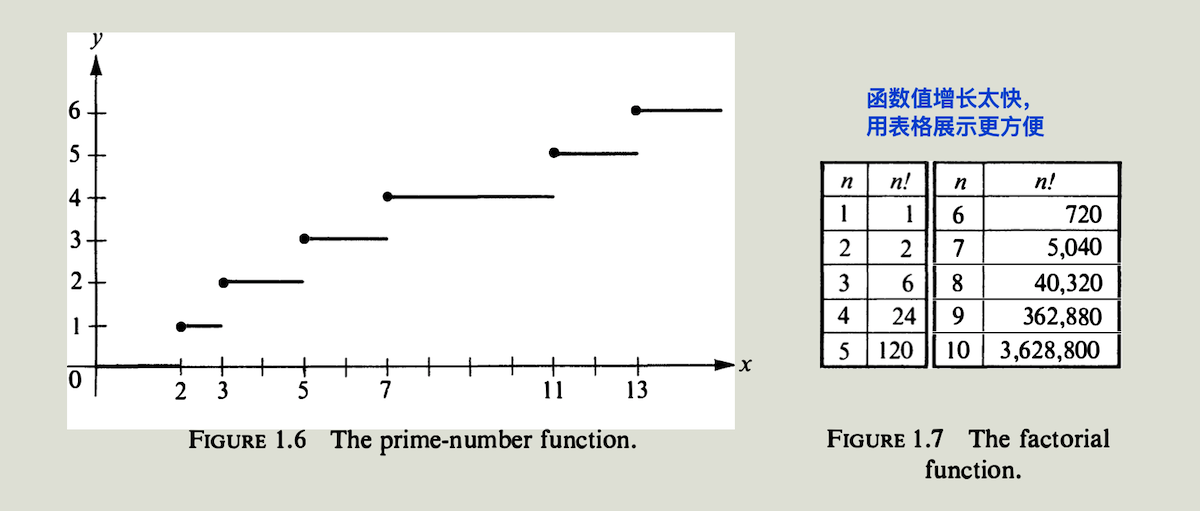
例6 素数函数 对任意$x>0$, 令$\pi(x)$ 表示小于或等于$x$的素数的个数. $\pi$ 的定义域是正实数集,值域是非负整数集 ${0,1,2,\cdots}$ . 部分图像见图$1.6$ (在$x$轴和$y$轴上使用了不同的尺度). 随着$x$增加,函数值保持不变直到达到一个素数。在素数点,函数值跳跃增加1. 因此函数$\pi$的图像由水平线段组成。这是阶梯函数的一个例子。阶梯函数在积分理论中具有重要作用。
例7 阶乘函数 对每个正整数$n$, 我们把$f(n)$ 定义为$n!= 1 \cdot 2 \cdot 3 \cdots n$. 函数$f$的定义域是正整数集. 函数值增长太快所以用表格形式表示比用图像表示更方便。图$1.7$展示了一张列举$n=1,2,3\cdots,10$时有序对$(n,n!)$ 的表格。
读者应该注意到以上这些例子具有两个共同的特征:
$(1)$ 对定义域$X$中的每个$x$, 有且仅有一个与这个特定的$x$匹配的像$y$. $(2)$ 每个函数产生一个有序对$(x,y)$组成的集合, 其中$x$是定义域$X$中的元素,而$y$是$Y$中与$x$对应的唯一元素.
在前面大多数例子中,我们用几何方法把有序对$(x,y)$ 表示为图像上的点,例7中则作为表格中的条目来展示。在各种情况下,了解一个函数就是用这样或那样的方式了解它所生成的所有有序对$(x,y)$. 这一简单的观察是函数概念的正式定义的motivation, 我们在下一节会讲到.
1.3 函数的正式定义: 作为有序对的集合
上节我们描述函数概念的一些用词如“关联”、“对应”不能准确地把相同的含义传递给所有人,我们将以集合的概念为基础,换一种方法重新阐述函数的定义。 首先我们需要了解对象的有序对的概念。
在集合相等的定义中,元素出现的顺序是无关紧要的,集合${2,5}$ 与集合${5,2}$ 是相等的,因为它们由相同的元素组成. 有时顺序也是重要的。例如在平面解析几何中,一个点的坐标$(x,y)$表示一对有序的数字. 坐标为$(2,5)$的点与坐标为$(5,2)$的点是不同的. 类似地,假设我们有一对对象$a$和$b$,如果我们要区分其中的一个与另一个,比方说把$a$作为第一个元而$b$作为第二个元, 我们就把对象放入括号中,写成$(a,b)$. 我们把它称为有序对. 我们说两个有序对$(a,b)$和$(c,d)$相等,当且仅当它们的第一个元相等且第二个元也相等. 也就是说:
现在我们来陈述函数的正式定义。
函数的定义 函数是一个有序对$(x,y)$ 的集合,其中不能存在两个有序对有相同的第一个元.
如果$f$是一个函数,作为有序对$(x,y)$ 第一个元的所有$x$的集合叫做$f$ 的定义域,作为第二个元的$y$的集合称为值域,也被称为$f$的值的集合 (set of values of $f$).
直观地,可以把函数看成由两列组成的表。表中的每个条目是一个有序对$(x,y)$; $x$的列是$f$的定义域,$y$的列是$f$的值域. 如果表中的两个条目$(x,y)$和$(x,z)$有相同的$x$值,则如果这个表是一个函数,必有$y=z$. 换句话说,一个函数不能在给定的点$x$取两个不同的值. 因此,对$f$定义域中的每个$x$, 有且仅有一个$y$使得$(x,y) \in f$. 因为只要$x$已知,这个$y$就是唯一确定的, 我们可以引入一个专门的符号,习惯上写成:
\(y = f(x)\)
而不是$(x,y) \in f$, 来表明有序对$(x,y)$是在集合$f$中.
除了直接列出所包含的有序对,通常还有另一种更好的方式来描述函数:先描述函数$f$的定义域,然后对定义域中每个$x$, 描述如何取得函数值$f(x)$. 关于这种描述,我们有以下定理:
定理1.1 两个函数$f$和$g$相等,当且仅当:
$(a)$ $f$和$g$具有相同的定义域, 并且
$(b)$ 对定义域中每个$x$ 都有 $f(x)=g(x)$.
还有一点很重要,应该意识到函数的有序对$(x, f(x))$ 中的$x$和$f(x)$不一定是数,它们可以是任何类型的任意对象。有时我们需要用到这种更具普遍性的概念,但多数情况下我们只对实函数感兴趣,也就是定义域和值域都是实直线的子集的那些函数.
注:用等式形式的表达式描述函数时,“=” 号的含义主要不是方程或其他等式中的“相等”之意,而应理解成“定义为”的意思。
1.4 实函数的更多例子
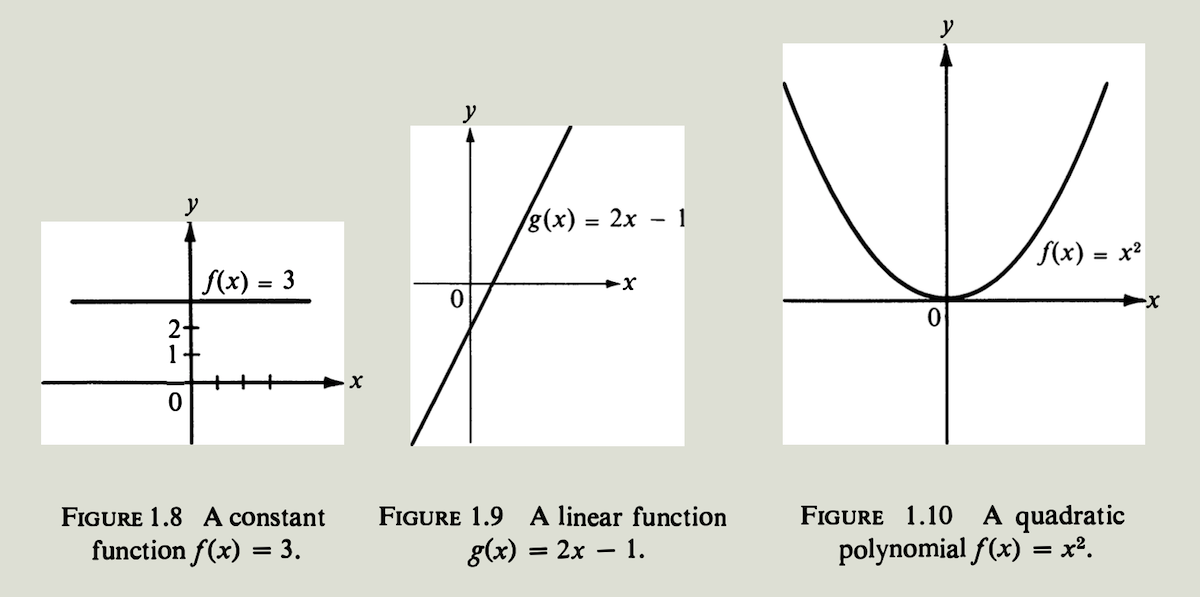
1. 常值函数 值域只由单一数字组成的函数叫做常值函数 (constant function). 图$1.8$ 给出一个例子,对每个实数$x$都有$f(x)=3$. 图像是一条与$y$轴相交于点$(0,3)$ 的水平线.
2. 线性函数 对所有实数$x$, 用公式
\[g(x) = ax + b\]定义的函数叫做线性函数,因为它的图形是一条直线. 数 $b$ 叫做直线在$y$轴的截距 (y-intercept), 它是直线与$y$轴交点$(0,b)$ 的纵坐标. 数$a$称为直线的斜率. 图$1.4$给出的是 $g(x)=x$ 的例子,图$1.9$给出另一个例子 $g(x)=2x-1$.
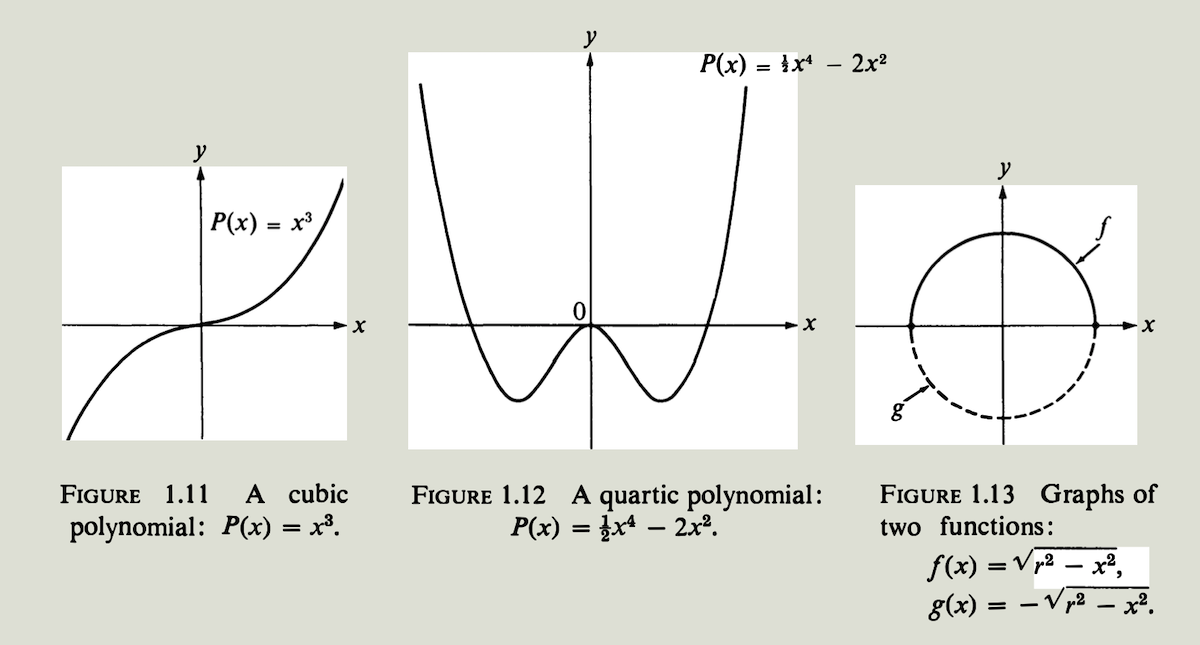
3. 幂函数 $n$是一个固定的正整数,对所有实数$x$,用等式$f(x)=x^n$ 定义函数$f$. 当$n=1$时,这是一个恒等函数,见图$1.4$. 当$n=2$时,图形是一条抛物线 (parabola),部分图像见图$1.10$. 当$n=3$时,图形是一条三次曲线 (cubic curve),外观见图$1.11$.
4. 多项式函数 多项式函数$P$是对所有实数$x$用形如
\[P(x) = c_0 +c_1x + c_2x^2 + \cdots + c_nx^n = \sum \limits_{k=0}^{n} c_k x^k\]的等式定义的函数. 常数$c_0, c_1, \cdots c_n$ 称为多项式的系数 (coefficients). 当$c_n \ne 0$时,非负整数$n$称为多项式的次数 (degree). 常值函数和幂函数其实只是多项式函数的特例。次数为$2, 3, 4$ 的多项式分别称为二次 (quadratic)、三次 (cubic) 和四次(quartic)多项式. 图$1.12$展示了由$P(x)=\frac{1}{2}x^4 - 2x^2$ 定义的四次多项式的图形.
5. 圆 回顾一下圆的笛卡尔方程$x^2+y^2=r^2$ 并用$x$表示$y$来解这个方程, 就得到两个解
\[y = \sqrt{r^2-x^2} \quad 和 \quad y = - \sqrt{r^2-x^2}\](提醒一下,如果$a>0$,符号$\sqrt{a}$表示$a$的正平方根,$-\sqrt{a}$是负平方根). 历史上有个时期数学家们习惯说$y$是由$y = \pm \sqrt{r^2-x^2}$ 给出的“双值”函数 (double-valued function) . 然而,更现代的观点不承认“双值”性作为函数的性质,函数的定义要求对于定义域中的每个$x$ 对应值域中唯一的一个$y$. 从几何上看,与图形相交的垂线恰好交于一点。为了符合函数的定义,我们说$y$的两个解定义了两个函数
\[f(x) = \sqrt{r^2-x^2} \quad 和 \quad g(x) = -\sqrt{r^2-x^2}\]其中$-r \le x \le r$. 两个函数的定义域都是$-r$到$r$的区间. 如果$\lvert x \rvert > r$, 则不存在使得$x^2+y^2=r^2$ 的实数$y$. 我们说函数$f$和$g$对这样的$x$没有定义. 因为$f(x)$是$r^2-x^2$的非负平方根,$f$ 的图形是图$1.13$中的上半圆;$g$ 的函数值$\le 0$, 所以$g$的图形是图$1.13$中的下半圆.
6. 函数的和、积与商 令$f$和$g$是有相同定义域$D$的两个实函数. 我们能通过加、乘或除函数值,从$f$和$g$构造新的函数. 由等式 \(u(x) = f(x) + g(x) \quad (x \in D)\) 定义的函数称为$f$与$g$的和, 并用$f+g$表示. 类似地,积 $v = f \cdot g$ 以及商$w = f/g$ 分别由公式
\[\begin{align} v(x) &= f(x)g(x) \quad (x \in D) \\ w(x) &= f(x) / g(x) \quad (x \in D \ 且\ g(x)\ne 0) \end{align}\]进行定义。