向量的叉积又称向量积/外积/矢积(区别于向量的点积/内积/标积)
叉积的标准介绍
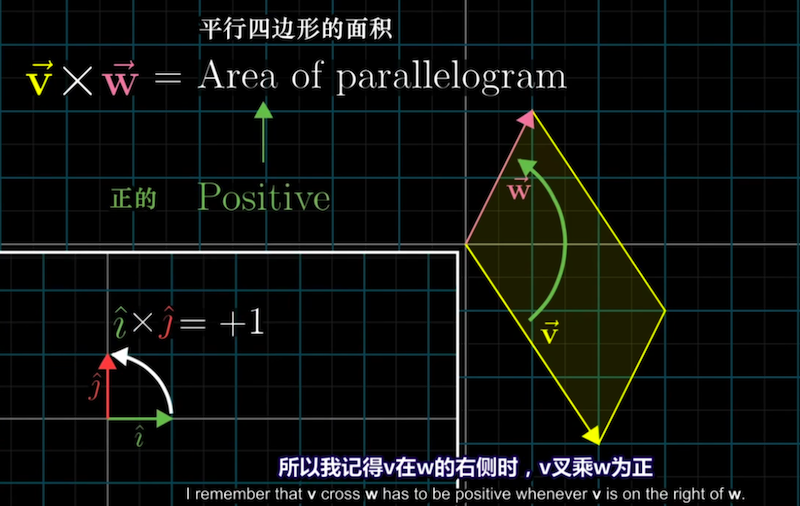
可以把二维向量的叉积定义为一个标量,表示两向量所围成平行四边形的有向面积。
叉积的正负由基向量$\hat{i} \times \hat{j} = +1$ 定义,运算符X左边的向量居右时为正。
则单位基向量之间的叉积运算有以下结果:$ \hat{i} \times \hat{i} = \hat{j} \times \hat{j} = 0 \quad \hat{i} \times \hat{j} = -\,\hat{j} \times \hat{i}$
可以证明,叉积运算满足分配律,即$\vec{a} \times (\vec{b}+\vec{c}) = \vec{a} \times \vec{b} + \vec{a} \times \vec{c}$
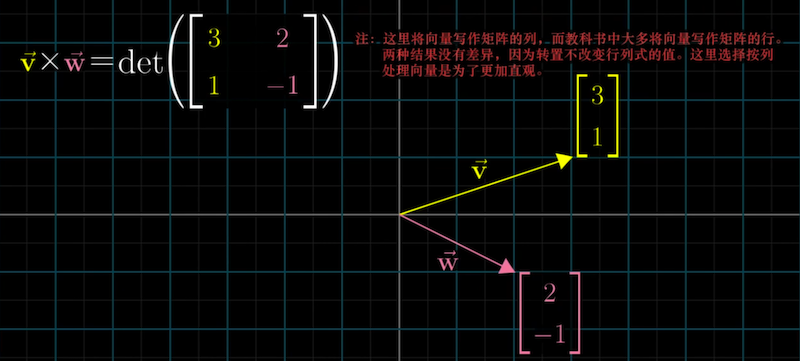
二维向量叉积的计算公式:只需把叉积的两个向量写为矩阵的列,
然后再求这个矩阵的行列式,即可得到所要求的平行四边形面积。
写为矩阵的行也可以,因为根据行列式的性质6,矩阵转置,行列式的值不变。
用矩阵行向量的叉积定义行列式,证明行列式性质6:\(\begin{vmatrix}a_x & a_y \\ b_x & b_y\end{vmatrix} = \begin{vmatrix}a_x & b_x \\ a_y & b_y\end{vmatrix}\)
Proof. 左边矩阵行向量 $a = (a_x, a_y) \quad b = (b_x, b_y)$
\(\begin{align} \begin{vmatrix}a_x & a_y \\ b_x & b_y\end{vmatrix}= a \times b &= (a_x\hat{i}+a_y\hat{j}) \times (b_x\hat{i}+b_y\hat{j})\\ &=a_x\hat{i} \times b_x\hat{i} + a_x\hat{i} \times b_y\hat{j}+ a_y\hat{j} \times b_x\hat{i} + a_y\hat{j}\times b_y\hat{j} \\ &= a_xb_x(\hat{i}\times\hat{i}) +a_xb_y(\hat{i}\times \hat{j}) + a_yb_x(\hat{j}\times \hat{i}) + a_yb_y(\hat{j}\times\hat{j}) \\ &=a_xb_y -a_yb_x \end{align}\)
右边矩阵行向量 $a’ = (a_x, b_x) \quad b’ = (a_y, b_y)$
\(\begin{align} \begin{vmatrix}a_x & b_x \\ a_y & b_y\end{vmatrix}= a' \times b' &= (a_x\hat{i}+b_x\hat{j}) \times (a_y\hat{i}+b_y\hat{j})\\ &=a_x\hat{i} \times a_y\hat{i} + a_x\hat{i} \times b_y\hat{j}+ b_x\hat{j} \times a_y\hat{i} + b_x\hat{j}\times b_y\hat{j} \\ &= a_xa_y(\hat{i}\times\hat{i}) +a_xb_y(\hat{i}\times \hat{j}) + b_xa_y(\hat{j}\times \hat{i}) + b_xb_y(\hat{j}\times\hat{j}) \\ &=a_xb_y -a_yb_x \\ &= \left|\begin{matrix} a_x & a_y \\ b_x & b_y \end{matrix}\right| \quad \# \end{align}\)
性质6的几何解释:两个向量的叉积等于这两个向量各垂直分量的叉积之和,
即叉积所得的有向面积之和。
二阶行列式几何直观如图3-10(a),行列式等于大四方形的面积减去小四方形的面积
转置后垂直分量 $a_x\hat{i} \times b_y\hat{j}$ 所得的正向面积 (图中的大四方形)不变,都为$a_1b_2$ ;
转置后另一对垂直分量从$a_y\hat{j} \times b_x\hat{i}$ 变为$b_x\hat{j} \times a_y\hat{i}$ 所得的小四方形进行了关于
y = x对称的镜像变化,所得的负向面积也不变, 都为$-a_2b_1$
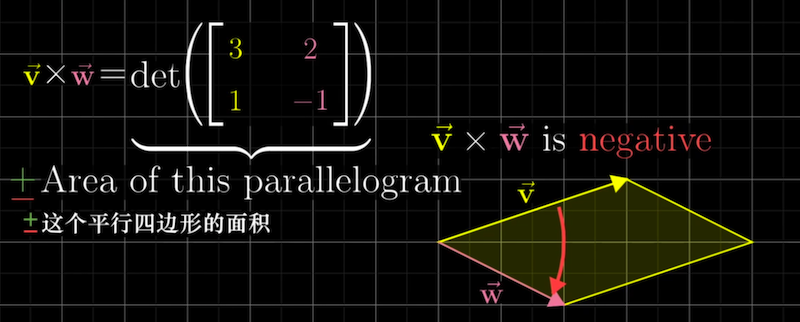
如果v在w的左侧,也就是变换后orientation改变了,那么行列式为负,叉积也为负。
两向量越接近垂直(夹角越接近90度) 叉积越大,两向量越接近同向(夹角越小),叉积越小,
因为两条边越接近垂直,平行四边形的面积$|a||b|sin\langle a, b\rangle$越大。

如果放大其中一个向量,比如把 $\vec{v}$ 放大为3倍,平行四边形的面积也同时放大3倍, 即$(3v) \times \vec{w} = 3(\vec{v} \times \vec{w}) $

真正的叉积只能定义在三维空间中,计算结果不是一个数,而是一个向量。
三维向量的叉积是通过两个三维向量生成一个新的三维向量,
其模长是两向量所夹平行四边形的面积,方向垂直于两向量所在平面。
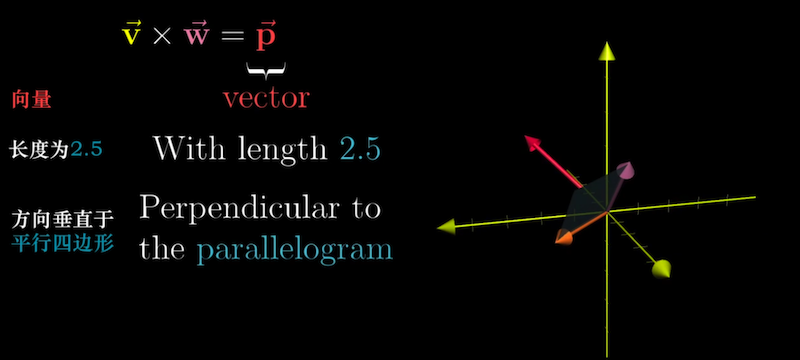
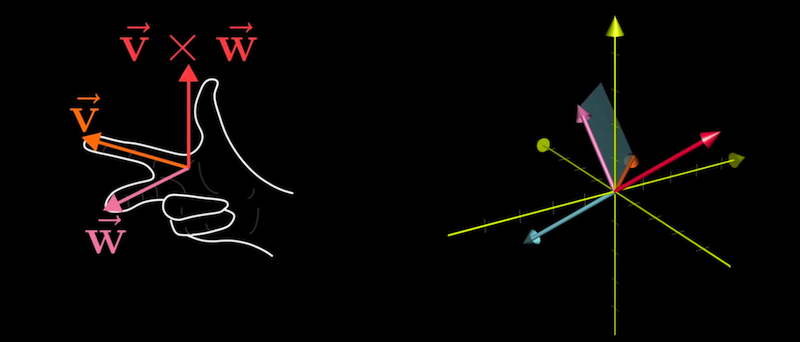
垂直于给定平面的向量有两个,具体是哪一个由右手定则确定。
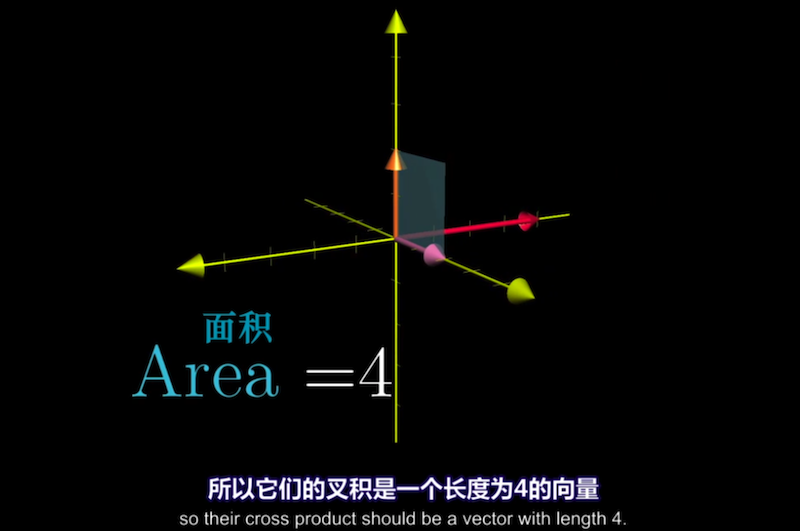
例如 $\vec{v}=(0, 0, 2) \quad \vec{w} = (0, 2,0)$ 则 $\vec{v} \times \vec{w} = (-4, 0, 0)$ 长度为4,方向为x轴负方向。
三维向量叉积的计算公式。结果是一个向量,表示为$i$, $j$, $k$的线性组合。

叉积的几何定义和几何解释
设三维空间中的两个向量$a = (a_x, a_y, a_z)$,$b = (b_x, b_y, b_z)$,则
\(\begin{align} a \times b &= |a||b|\sin{\theta}\,n_0 \quad 叉积的几何定义式,\,其中n_0是垂直于a和b展成平面的单位法向量 \\ a \times b &= (a_yb_z-a_zb_y,\ a_zb_x-a_xb_z,\ a_xb_y-a_yb_x) \quad 叉积的坐标公式\end{align}\)
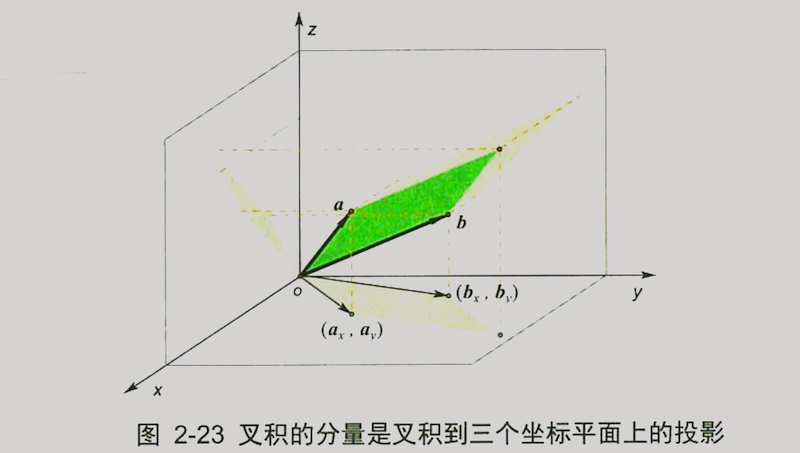
两个三维向量$a$ 和 $b$ 在空间中张成一个平行四边形面积块,叉积坐标公式中的三个分量
就是这个平行四边形分别在yOz、xOz和xOy平面上的投影。这三个坐标数字的几何意义
就是 $a$ 和 $b$ 在三个坐标平面上投影向量所夹的有向面积,由两个投影向量的叉积计算得出。
例如第三个分量$a_xb_y -a_yb_x$就是在xOy平面上的投影,计算两个投影向量$(a_x,\,a_y)$和$(b_x,\,b_y)$
的叉积 $(a_x,\,a_y) \times (b_x,\,b_y)$ 即行列式 \(\left|\begin{matrix} a_x & a_y \\ b_x & b_y \end{matrix}\right|\) 可得到投影的有向面积。
再如第二个分量是在xOz平面上的投影,因为投影变换后的基向量 $\hat{i}$ 在x轴方向上, $\hat{k}$在z轴方面上,
$\hat{i}$在$\hat{k}$的左侧而不在右侧,根据右手定则,$\hat{i} \times \hat{k} = -1$,则投影向量的叉积表示的是负向面积,
$(a_x,\, a_z) \times (b_x,\,b_z) = (a_x\hat{i} +a_z\hat{k}) \times (b_x\hat{i}+b_z\hat{k}) = a_xb_z(\hat{i} \times \hat{k}) + a_zb_x(\hat{k} \times \hat{i}) $
也就是$a_zb_x - a_xb_z$ 即\((-1)\left|\begin{matrix} a_x & a_z \\ b_x & b_z \end{matrix}\right|\)
以线性变换的眼光看叉积

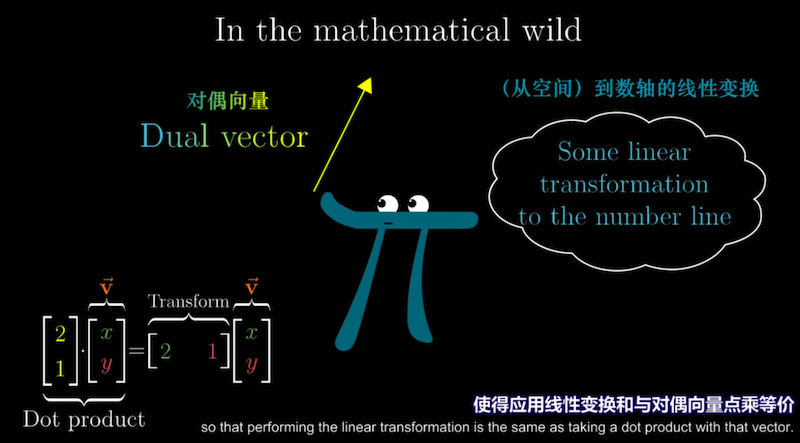
回顾线性变换与向量的对偶关系:任何n到1维的线性变换,都对应n维空间中唯一一个向量,
称为对偶向量,对输入向量应用变换 $\iff$ 对偶向量与输入向量作点积。
这是因为这类线性变换可由一个只有一行的矩阵描述,每一列给出了变换后基向量的位置。
将1xn矩阵与输入的n维向量相乘, 计算上与转置矩阵所得向量与n维向量点乘完全相同。
结论是每当你看到一个从n维空间到数轴的线性变换,都能找到唯一的对偶向量来作等价的点积运算。
仿照线性变换与点积的对偶关系,尝试定义一个3d-to-1d的变换,
找到它的对偶向量,并证明这个对偶向量就是叉积。

理解了这个线性变换就理解了叉积的行列式计算公式所代表的几何意义
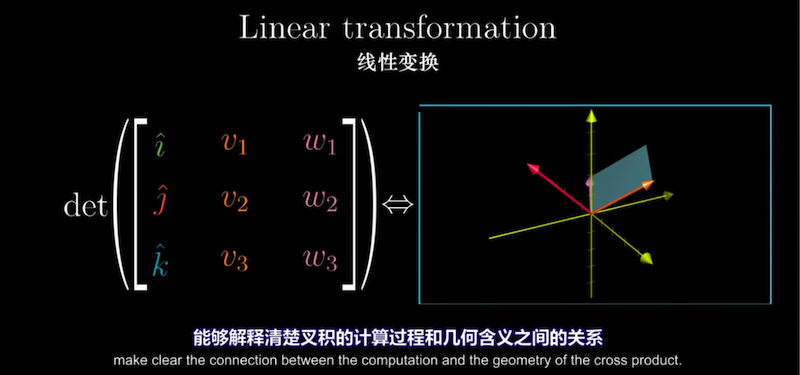
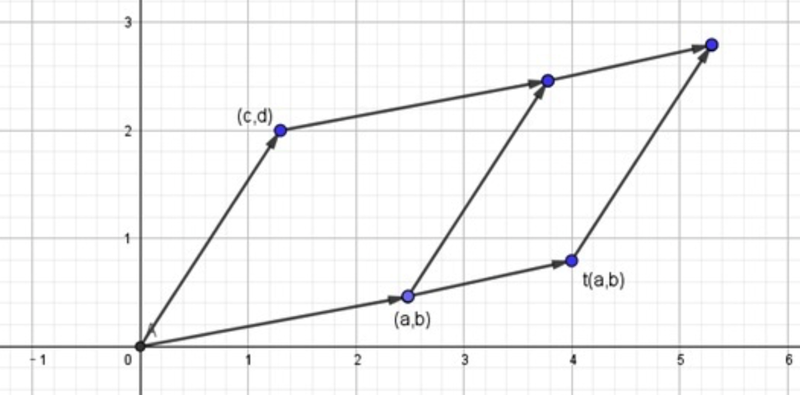
先来回顾二维向量的叉积,$v \times w$是以$v$和$w$为列(行)的行列式,表示两向量张成的
平行四边形有向面积, 符号由$v$和$w$相对位置决定。(右手定则,v在w右侧时为正)
仿照二维向量叉积的概念推广到三维的情况, $u \times v \times w= det\left(\left[\begin{matrix}u & v & w\end{matrix}\right]\right)$
表示三个向量张成的平行六面体的有向体积。
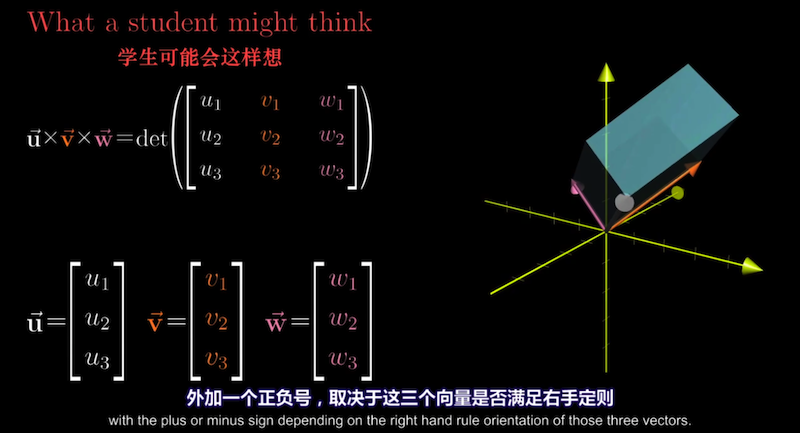
真正的叉乘运算接收两个向量输出一个向量,而不是接收三个向量输出一个数。
将第一个向量u看成可变向量$(x, y, z)$,其他两向量不变, 就有了一个从三维空间到一维数轴的函数,
这函数的几何意义是,对任意输入的向量$(x, y, z)$, 考虑它与常向量v和w张成的平行六面体体积。
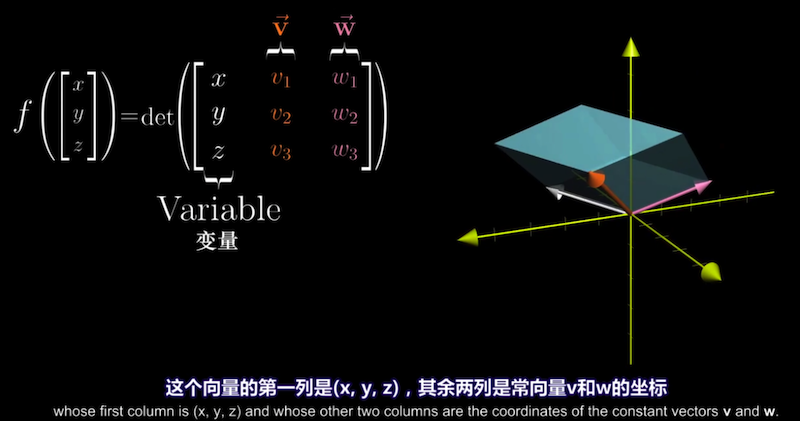
这个函数最重要的性质是它是线性的。 根据行列式的性质3可证$f(x,y,z)$是线性的。
性质3a 行列式对单独任一行(列)满足线性关系:
\(\left|\begin{matrix} ta & tb \\ c & d \end{matrix}\right| = t\left|\begin{matrix} a & b \\ c & d \end{matrix}\right|\ , \quad \forall \,t \in \mathbb{R}\)
几何解释就是将一行或列向量缩放t倍,其他向量不变,张成的面积块也缩放缩放为原来的t倍。
性质3b 加法可拆性:
\(\left|\begin{matrix} a+a' & b+b' \\ c & d \end{matrix}\right| = \left|\begin{matrix} a & b \\ c & d \end{matrix}\right|+ \left|\begin{matrix} a' & b' \\ c & d \end{matrix}\right|\)
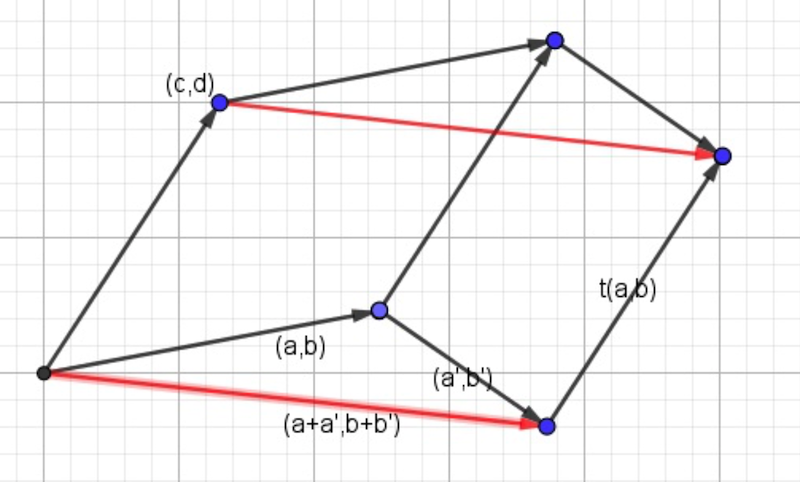
所以该变换满足$L(v+w) = L(v)+L(w)$ 和$L(cv) = cL(v) $的严格线性性质,是一个线性变换。
一旦确定它是线性的,就可以用矩阵乘法来描述这个函数。
因为这个变换输入3D向量输出1D数字,表示变换的是1x3矩阵。
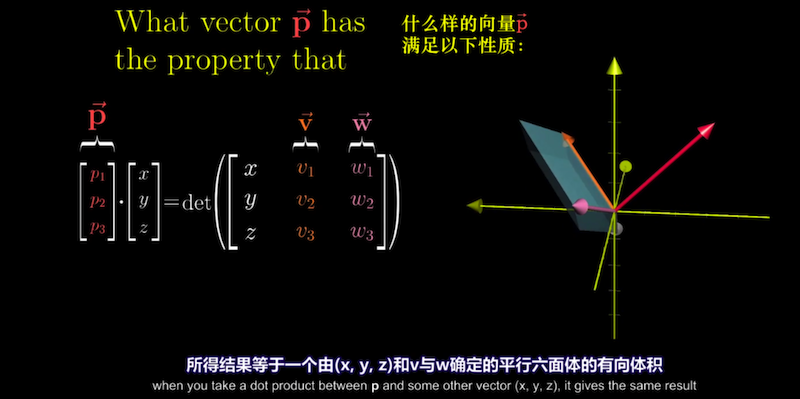
矩阵立起来得到的向量,就是线性变换的对偶向量,应用变换可看成与对偶向量作点积

我们要找的就是这个对偶向量$p = (p1,\,p2,\,p3) $使得它与$(x, y, z)$的点积等于定义的三阶行列式。
从代数的角度来找对偶向量$p$,右边行列式展开得到的$v$和$w$在各个坐标轴方向分量坐标的特定组合,
就是对偶向量p的坐标。

无论第一列是$(x,\,y,\,z)$还是$(\hat{i},\,\hat{j},\,\hat{k})$,展开行列式再合并各项得到向量坐标的运算过程都没有区别。
代入$\hat{i},\hat{j},\hat{k}$ 表示为基向量的线性组合只是一种计算技巧,强调结果是一个对偶向量,
权重系数$v_yw_z-v_zw_y$, $v_zw_x-v_xw_z$和$v_xw_y-v_yw_x$就是对偶向量的坐标。
如果换成$x, y, z$即可得到平行六面体的体积。
只要找到了对偶向量的坐标,对任意输入的三维向量$(x, y, z)$,只要与对偶向量作点积,
马上可算出所生成的平行六面体的体积。

下面从几何的角度来找出对偶向量$p$
$p$与$(x, y, z)$点积的几何意义是将$(x, y, z)$投影到p上,然后将投影长度与p的长度相乘。
再联系一下等式右边行列式的几何意义,即三向量张成的平行六面体的体积。
右边线性函数要与左边点积等价,必是一个3维到1维的投影变换,作用是把(x, y, z)
投影到p所在直线上, 再将投影长度与p长度相乘恰好得到行列式表示的体积。
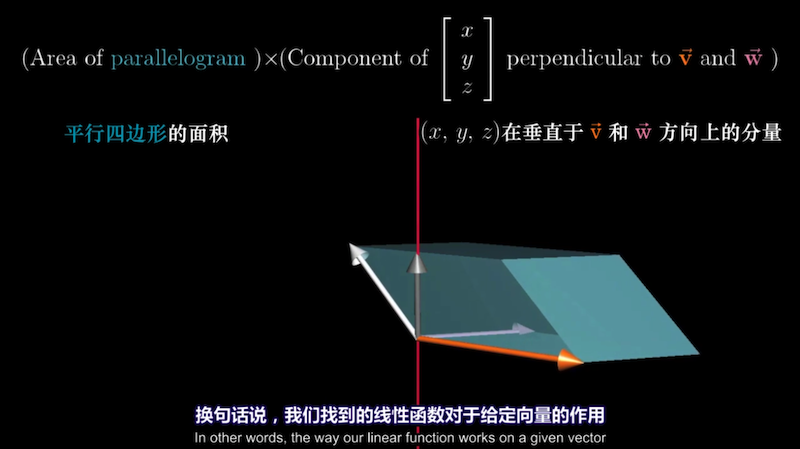
所以当向量p的长度恰好等于v和w张成的平行四边形面积、p的方向垂直于v和w且满足右手定则时,
以上等价关系成立,此时p是对偶向量。
这就得到了叉积$v \times w$的几何解释。叉积实际上是一个对偶向量,它和输入向量做点积运算,就是
在计算输入向量和两常向量张成的平行六面体体积,这个平行六面体的有向体积也就是混合积
$(v \times w) \cdot (x,y,z) $的几何意义。
