向量的点积又称数量积、内积。点积有两种定义方式:代数方式和几何方式。
向量的点积既可以由向量坐标的代数运算得出,也可以引入向量的长度和夹角的几何概念来求解。
二维向量的点积 $a \cdot b = x_1x_2 + y_1y_2 = | a | | b |\cos{\theta}$
无论根据哪一种定义都容易证明点积运算满足交换律和分配律 (不满足结合律)。
下面证明两个定义的等价性。
从几何定义推导坐标公式
设$a = (x_1, y_1)$, $b = (x_2, y_2)$, $\hat{i}$, $\hat{j}$为单位基向量,
由点积的几何定义 $\hat{i} · \hat{i} = | \hat{i} || \hat{i} | \cos{0} = 1, \quad \hat{j} · \hat{j} = | \hat{j} | | \hat{j} | \cos{0} = 1$,
$\hat{i} · \hat{j} = | \hat{i} | | \hat{j} | \cos{\dfrac{\pi}{2}} = 0$,
由向量坐标的定义,$a = x_1\hat{i} + y_1\hat{j}, \quad b= x_2\hat{i} + y_2\hat{j} $ ,
$\because$ 点积满足分配率
\(\begin{align} \therefore a \cdot b &= (x_1\hat{i}+y_1\hat{j})\cdot(x_2\hat{i}+y_2\hat{j}) \\ &=x_1x_2(\hat{i}\cdot\hat{i})+x_1y_2(\hat{i}\cdot\hat{j})+x_2y_1(\hat{i}\cdot\hat{j})+y_1y_2(\hat{j}\cdot\hat{j}) \\ &= x_1x_2 + y_1y_2 \end{align}\)
从坐标定义推导几何公式 (推广到n维)
n维向量夹角的定义
设$a$和$b$为两个任意非零n维向量,以$a$,$b$,$a-b$ 三向量的模长为边可构成三角形。
(利用三角不等式$|x + y| \le |x| + |y|$证明任意两边之和大于等于第三边,即可证能构成三角形)
向量$a$和$b$的夹角定义为这个三角形中长为$|a|$和$|b|$的两邻边夹角$\theta$。
由余弦定理,$|a-b|^2 = |a|^2 + |b|^2 - 2|a||b|\cos{\theta}$
由点积的坐标定义,
\(\begin{align}|a - b|^2 &= (a - b) \cdot (a - b) \\ &= a \cdot a - a \cdot b - b \cdot a + (-b) \cdot (-b) \quad (点积满足乘法分配律)\\ &= |a|^2 - 2(a \cdot b) + |b|^2 \qquad (1) \\ &= |a|^2 + |b|^2 - 2|a||b|\cos{\theta} \qquad (2) \end{align}\)
等式$(1)(2)$两边消去得:$a \cdot b = |a|\,|b|\cos{\theta}$
补充1:n维向量正交的概念
基于n维向量夹角的定义,定义n维向量垂直的概念:
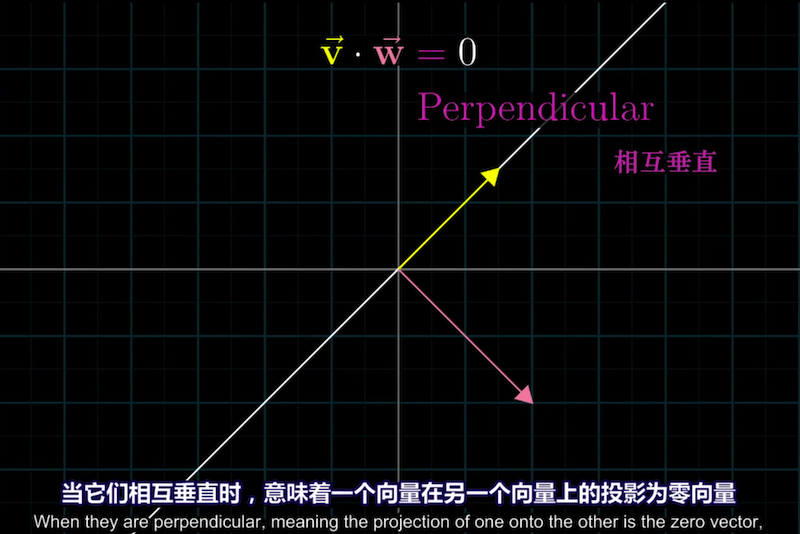
若两非零向量$a$和$b$夹角为90度则称$a$和$b$互相垂直。
由点积的几何公式有$a \cdot b = 0$ 即 两向量垂直 $\iff$ 两向量点积为0
零向量与任何向量正交。
补充2:余弦定理的证明
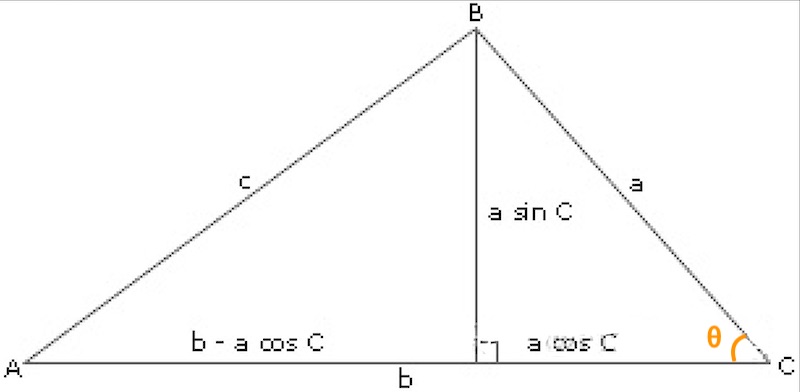
如图,由勾股定理:
\(\begin{align} c^2 &= (a\sin{\theta})^2 + (b-a\cos{\theta})^2 \\ &= a^2\sin^2\theta + b^2 - 2ab\cos\theta + a^2\cos^2\theta \\ &= a^2(\sin^2\theta + \cos^2\theta) + b^2 - 2ab\cos\theta \\ &=a^2 + b^2 - 2ab\cos\theta \end{align}\)
补充3: Cauchy-Schwarz不等式
不等式$|x \cdot y | \le |x|\,|y|$ 对$\forall$ 非零向量$x,y \in \mathbb{R}$都成立,
当且仅当$x = cy$时,即$x,y$共线时等号成立。
证明: 根据点积的性质 (向量自身的点积等于模长的平方),
注意到$\forall \,t \in \mathbb{R}$ 都有 $(x+ty)\cdot(x+ty) = |x+ty|^2 \ge 0$
$(x+ty)\cdot(x+ty)=x\cdot x+x\cdot ty+ty\cdot x +ty \cdot ty$
$= |x|^2 + 2t(x\cdot y) + t^2|y|^2 \ge 0$
以$t$为自变量变形为二次不等式:$p(t) = |y|^2t^2 +2(x\cdot y)t + |x|^2 \ge 0$
令$a = |y|^2,\,b = 2(x \cdot y),c=|x|^2$
$\because y$是非零向量 $\therefore a = |y|^2 > 0$ $p(t)$开口向上
$\because p(t) \ge 0 $ $\therefore$ 一元二次方程根的判别式$\,\Delta = b^2-4ac \le 0$
代入得:$[2(x \cdot y)]^2 -4|y|^2|x|^2 \le 0$
$4(x \cdot y)^2 - 4|x|^2|y|^2 \le 0$ 即 $|x \cdot y| \le |x|\,|y|$ 恒成立。
(根据点积的几何定义也可证明)
补充4:三角不等式
三角不等式: $|\vec{v}+\vec{w}| \le |\vec{v}|+|\vec{w}|$ 等号成立当且仅当其中一向量 为另一向量的非负倍数。 \(\begin{align} \textbf{证明:}|\vec{v}+\vec{w}|^2 &= (\vec{v}+\vec{w})\cdot(\vec{v}+\vec{w})=|\vec{v}|^2+2\underline{\vec{v}\cdot\vec{w}}+|\vec{w}|^2 \hspace{50em} \\ &\le |\vec{v}|^2+|\vec{w}|^2+2|\vec{v}\cdot\vec{w}| \\ &\le |\vec{v}|^2+|\vec{w}|^2+2|\vec{v}||\vec{w}| \quad (\text{Cachy-Schwarz}不等式)\\ &=(|\vec{v}|+|\vec{w}|)^2 \end{align}\) $\therefore |\vec{v}+\vec{w}| \le |\vec{v}|+|\vec{w}|$ 等号成立当且仅当$\vec{v}\cdot\vec{w}=|\vec{v}||\vec{w}|$,
这等价于$\vec{v},\vec{w}$其中一向量是另一向量的非负倍数。
注:基于Cauchy-Schwarz不等式可证明三角不等式,基于三角不等式
可定义n维向量夹角,从而推出向量点积的几何公式。
向量点积的几何直观
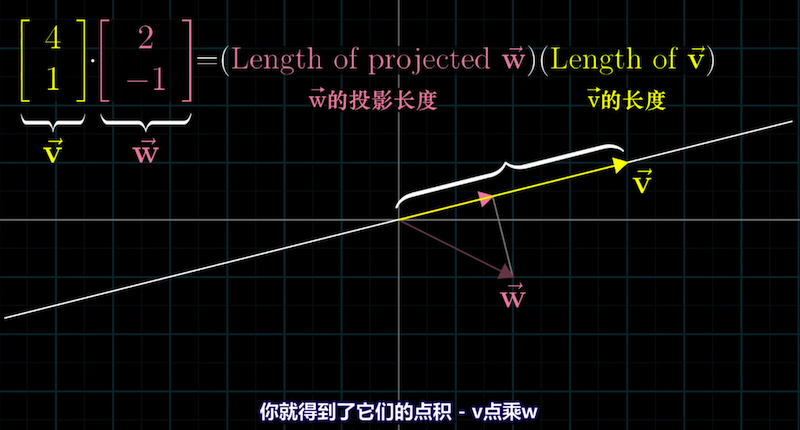
向量长度和另一向量投影长度之积
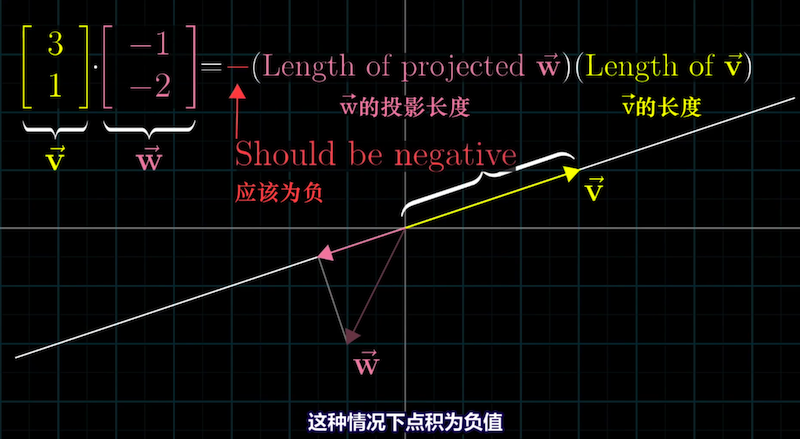
投影方向与被投影向量相反时,即两向量夹角大于90度时,点积为负值
当两向量互相垂直时,投影为零向量,点积为0
用投影解释向量点积的几何公式显得很”不对称”,因为$a$投影到$b$还是$b$投影到$a$都不影响计算结果。
为什么点积的结果与投影的方式无关呢?
先来看两向量等长的情况,沿着夹角平分线作对称轴,分别画出两向量之间的投影,
根据三角形全等的条件(两角一边),发现两种投影方式互为镜像,这种情况显然不影响结果。

现在把其中一个向量缩放若干倍。如下图,把短的向量投影到长的向量上,
此时$(k\vec{v})\cdot \vec{w} = k(\vec{v} \cdot \vec{w})$,因为缩放一个向量k倍并不会改变另一个向量的投影长度,
相当于把原来对称情况下的点积乘以k倍。

反过来把长向量投影到短向量上,根据相似三角形,$\vec{v}$ 在 $\vec{w}$上的投影被放大了2倍,
对短向量长度仍不变,相比镜像对称的情况,效果仍然是把原来的点积放大了2倍。
因此,无论哪种投影方式,缩放向量(破坏对称)对点积结果的影响都一样,
也就是说即使向量不等长,投影方式不同也不影响点积的结果。
直观理解坐标公式与几何投影的联系
假设我们不知道点积的几何定义,仅知道点积的坐标公式。
为什么将对应坐标相乘再将结果相加的计算过程,与投影有联系?
最令人满意的答案来自对偶性(duality)。
这种点积与投影(线性变换)的关系在于将其中一向量倾倒,
就得到对另一向量作投影变换的$1 \times n$矩阵。
首先来看多维空间到一维空间(数轴)的线性变换。
不少函数都能接收2维向量并输出一个数,但线性变换的要求更加严格,
需满足性质$L(\vec{v}+\vec{w}) = L(\vec{v})+L(\vec{w})$和$L(c\vec{v}) = cL(\vec{v})$
本篇仅考虑与之等价的直观特性,即“保持原点不变且网格线平行等距分布”,二维到一维的
变换情况就是任意二维向量所在直线上等距分布的点,经过线性变换后也等距分布于数轴上。
变换后的基向量落在数轴上变成一个数,用一个$1 \times 2$矩阵描述。

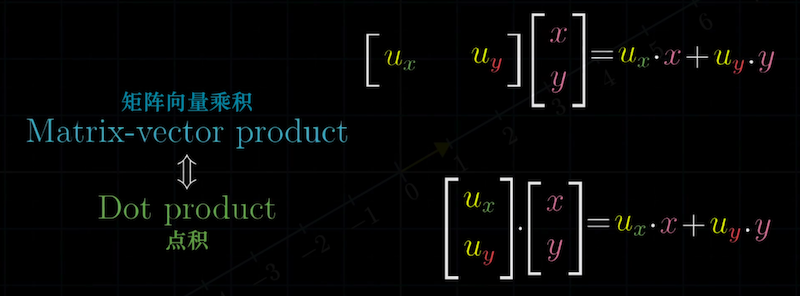
$\mathbb{R}^2 \rightarrow \mathbb{R}$的线性变换用$1 \times 2$矩阵与向量的乘法描述,其运算方法(列的线性组合)
看起来就和点积的坐标公式一样。$1 \times 2$矩阵看起来正像一个倾倒的向量。
通过以上观察发现,点积的坐标公式与$\mathbb{R}^2 \rightarrow \mathbb{R}$变换的$1 \times 2$矩阵向量乘法运算具有相同的形式。
下面我们从几何直观上验证一下2D投影矩阵左乘2D向量其实就是2D投影矩阵的行向量与
这个向量的对应坐标相乘再相加,从而确定点积的几何解释就是投影长度与向量模长之积。
假定你还不知道点积与投影有关,考虑0在原点斜放的数轴上一个单位向量(模长为1的向量)$\hat{u}$

如果我们把二维向量投影到这条数轴上,就定义了一个从二维向量到数字的变换,
通过视觉上的检验,发现这个投影变换是线性的。(直线上等距分布的点投影到数轴上仍保持等距)
注意u帽是输入空间中一个二维向量,只是刚好让它落在输出空间数轴上。
下面我们来找出这个投影变换对应的投影矩阵。

考虑变换后单位基向量$i$帽和$j$帽的位置,它们将分别变成矩阵的两列(两个数)。
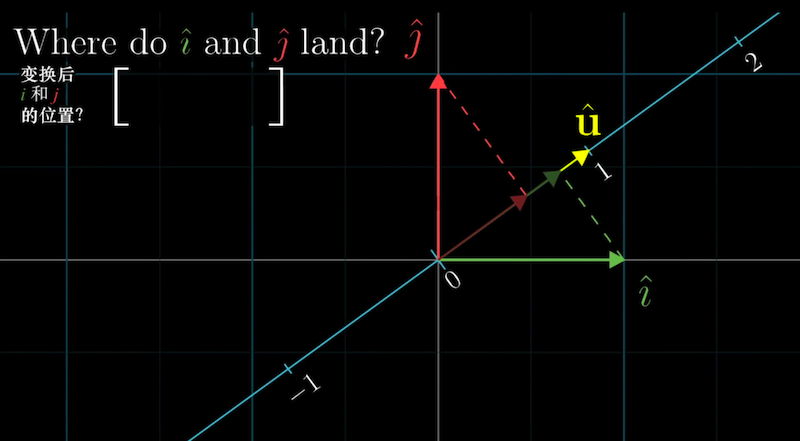
因为$\hat{i}$ 和 $\hat{u}$都是单位向量,它们之间的互相投影存在之前提到过的镜像对称关系,
$\hat{i}$在$\hat{u}$上的投影长度其实就是$\hat{u}$的横坐标$u_x$,同理,$\hat{j}$ 在$\hat{u}$上的投影长度等于$\hat{u}$的纵坐标$u_y$

因此投影变换矩阵就是$\bigl[\begin{matrix} u_x & u_y \end{matrix}\bigr]$,所以任意二维向量与单位向量的点积,
都可解释为将向量投影到单位向量所在直线上所得到的投影长度(可正可负)
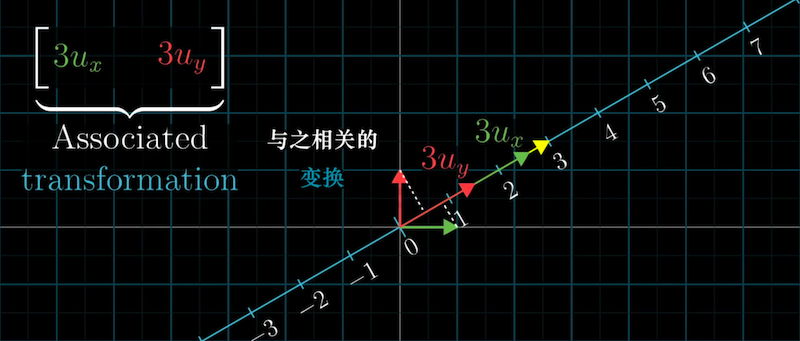
如果是与“非单位向量”的点积,对偶的变换是$\bigl[\begin{matrix} ku_x & ku_y \end{matrix}\bigr]$,即基向量的投影长度分别是$u_x$和$u_y$的$k$倍。
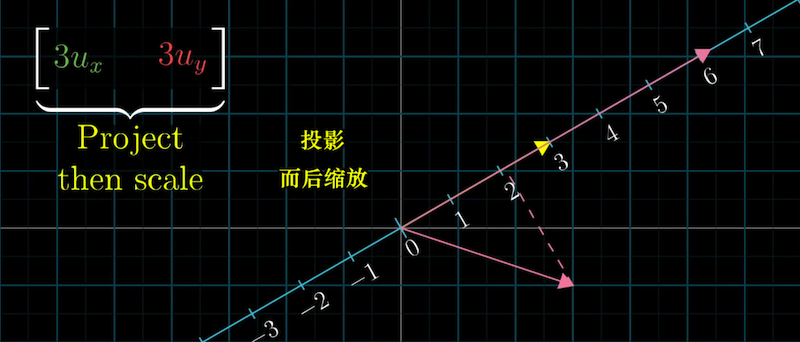
因为变换是线性的,即$\bigl[\begin{matrix} ku_x & ku_y \end{matrix}\bigr] = k\bigl[\begin{matrix} u_x & u_y \end{matrix}\bigr]$, 这个变换等价于先将二维向量投影到单位向量,
再把投影长度乘上k倍。单位向量的缩放倍数k即“非单位向量”的模长,所以任意两个向量点积的
几何解释就是投影长度与向量长度的乘积,从而得到点积的几何公式$|a||b|\cos{\theta}$
对点积的直观几何解释用到了对偶性的思想。
对偶性是两个数学事物之间存在的自然而又出乎意料的对应关系。
两个向量的点积,利用向量与线性变换的对偶关系,相当于把其中一个向量看作是投影变换矩阵。
于是,我们可以进一步地理解向量的本质是“线性变换的物质载体”。
(as the physical embodiment of a linear transformation”)
向量就像一个特定变换的概念性记号,例如本节中转置成$1 \times 2$矩阵的二维向量就是投影变换的记号。
一个2d-to-1d的线性变换,必存在一个唯一的向量,
输入向量与这个对偶向量点积与应用变换的效果是一样的。
duality 这个概念在数学和物理的许多地方都有分布,而没有一个统一的定义。我熟悉的 duality 大部分都是
把两个显然相对应的东西联系起来,有时这两个东西在某种程度上甚至是等价的(比如在同构意义上)。
因为一旦有了对偶性,每证明一个定理都能通过对偶的操作自动免费得到另一个(可以理解为镜像)。
数学的布尔代数和集合论中的对偶概念可能是最平易近人的。
物理中常翻译为二象性,例如波粒二象性 (Wave–particle duality)。
