P5 矩阵乘法与线性变换复合
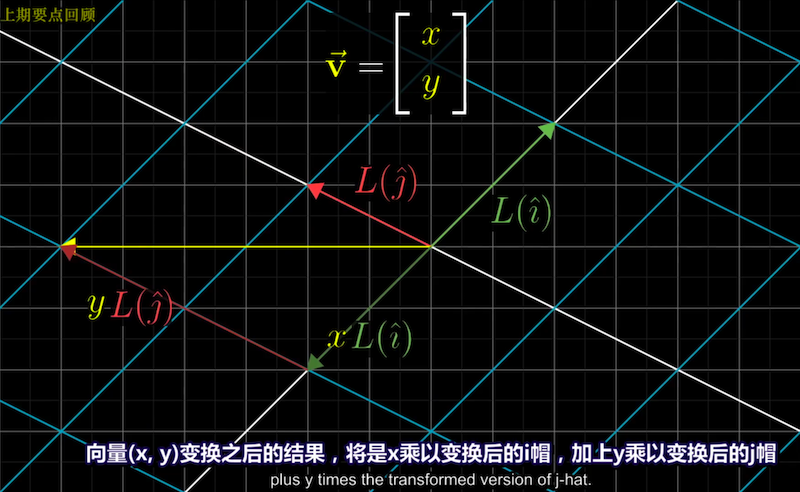
线性变换$L(\vec{\mathbf{v}})$是将向量作为输入和输出的一类函数,线性变换
“保持网格线平行且等距分布”的性质有个绝妙的推论:
$\vec{\mathbf{v}} = (x, y) \qquad L(\vec{\mathbf{v}}) = xL(\hat{\mathbf{i}}) + yL(\hat{\mathbf{j}})$
即线性变换完全由变换后的基向量决定。 在新的坐标系中,
变换后的向量与变换后的基向量仍然满足相同的线性关系。
Proof. 已知 $\vec{v} = x\hat{i}+y\hat{j}$ ,$L(x)$ 是线性函数,由线性函数的可加性和比例性
(和的函数的函数的和,比例的函数等于函数的比例):
\(\hspace{5em}L(\vec{v}) = L(x\hat{i}+y\hat{j}) =L(x\hat{i})+L(y\hat{j})=xL(\hat{i})+yL(\hat{j})\)
习惯上,将变换后的基向量$\hat{\mathbf{i}}$ 和 $\hat{\mathbf{j}}$ 作为矩阵的列 $[L(\hat{\mathbf{i}})\quad L(\hat{\mathbf{j}}) ]$ 并将$xL(\hat{\mathbf{i}}) + yL(\hat{\mathbf{j}})$定义为矩阵向量乘法。
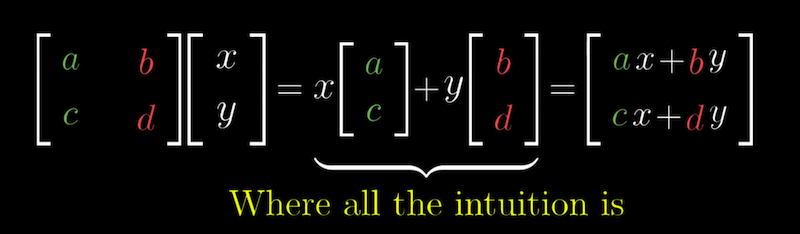
这样,矩阵就代表了一个特定的线性变换,
矩阵乘上一个向量,意味着将线性变换作用于那个向量。
复合变换的例子:先旋转后剪切

两个矩阵相乘的几何意义,就是两个线性变换相继作用。
两个独立变换相继作用 $\Longleftrightarrow$ 一个复合变换
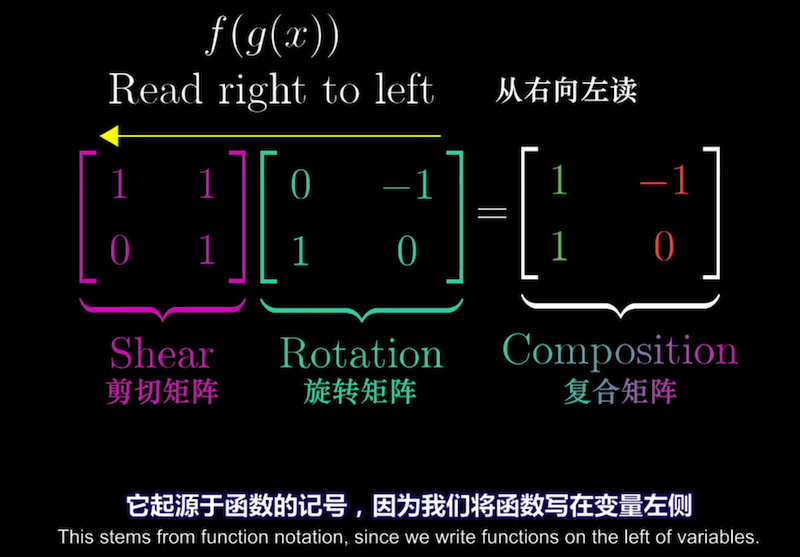
矩阵相乘数值计算的几何直观:基向量最终落在了哪里?
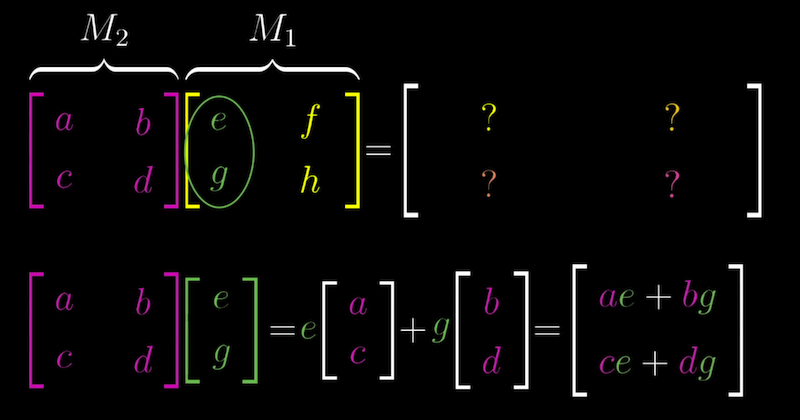
第一个变换的基向量($\mathbf{M}_1$的列向量) 在第二个变换M2的作用下,
最终得到复合变换的基向量 (复合矩阵的列)
把右边的矩阵看成输入向量(基向量),左边矩阵看成一个线性变换,
相乘结果矩阵每一列是输出向量(最终变换后的基向量)
矩阵乘法不满足交换律: $\mathbf{M}_1\mathbf{M}_2 \ne \mathbf{M}_2\mathbf{M}_1$
(想象i帽和j帽 “先旋转后剪切”和“先剪切后旋转”最终基向量的明显不同)
矩阵乘法满足结合率:$(\mathbf{AB})\mathbf{C} = \mathbf{A}(\mathbf{BC})$
(用数值方法证明太麻烦,符号证明即可,从几何意义的角度看,结论是trivial的。
括号不影响结果,无论先算哪个乘积, 实际上都是从右向左依次进行C, B, A变换,
等式两边的变换是等效的)
P6 补充:三维空间中的线性变换
三维矩阵相乘在计算机图形学、机器人学等领域有重要应用,
因为三维空间中的复杂旋转等变换可以分解成简单旋转变换的复合。 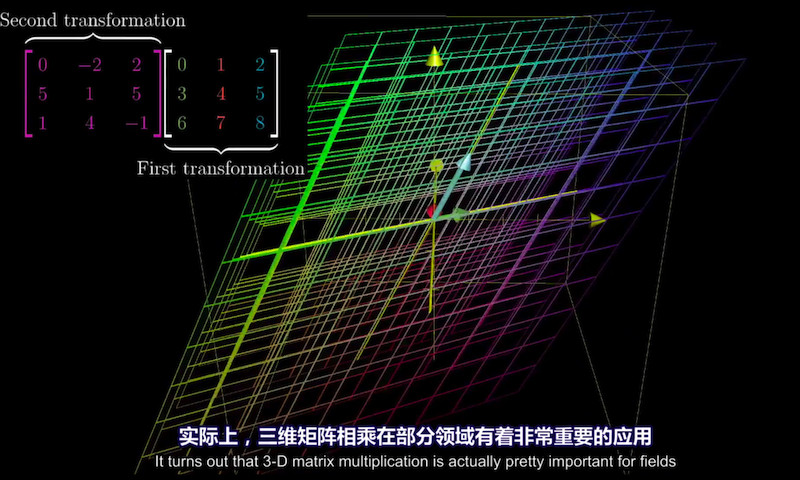
P7 行列式 determinant
问题:如何测量一个变换对空间的拉伸/挤压程度?
更具体地说,就是测量一个给定区域的面积被缩放的比例。 二维行列式的几何直观是面积,看变换后的基向量所夹面积 / 单位向量所夹正方形面积(=1) 即矩阵各列向量所夹面积 
只要知道单位正方形面积变化的比例,就能知道其他任意区域的面积变化比例 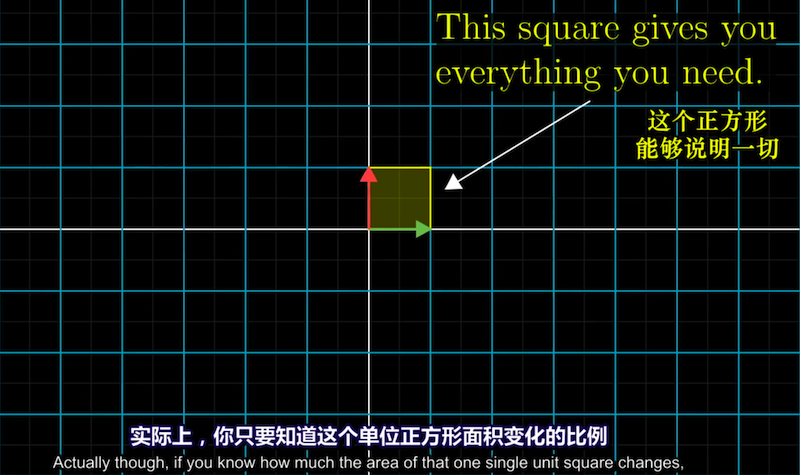
因为一个方格面积缩放多少倍,其他大小的方格也会跟着缩放多少倍,
这是由“线性变换保持网格线平行且等距分布”这一性质推断出的。

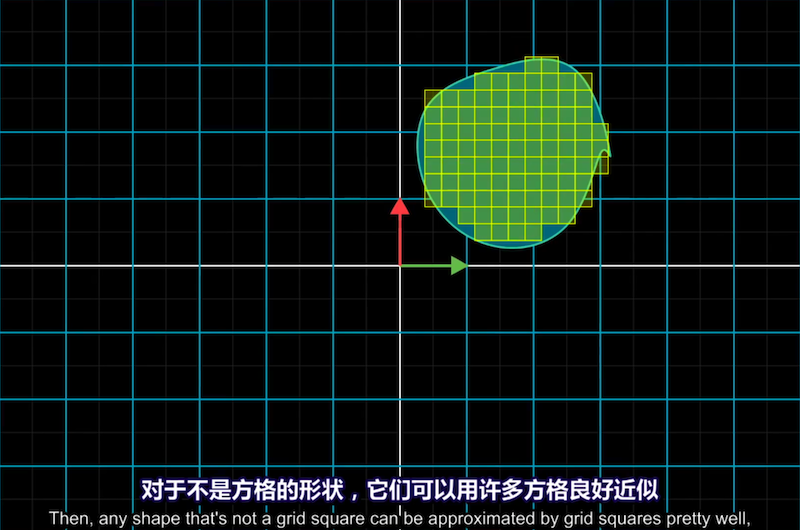
对不是方格的形状,可以用多个方格近似。因为所有小方格都进行了同样比例的缩放,
所以整个不规则图形也进行了一样比例的缩放。
一个变换的determinant $\Longleftrightarrow$ 一个矩阵的行列式

行列式为0的几何意义
意味着矩阵表示的变换将空间压缩到更小的维度。(二维的情况是压缩到一条直线或原点)
因此,只要检验矩阵的行列式是否为0,就能知道矩阵代表的变换是否将空间压缩到更小的维度。 
行列式为负值的几何直观
想象把一张纸翻转到另一面。基向量$\hat{j}$变换到了基向量$\hat{i}$的右侧, 即$L(\hat{j})$在$L(\hat{i})$右侧,
视觉上就是把整个平面空间翻转过来 (invert the orientation of space)

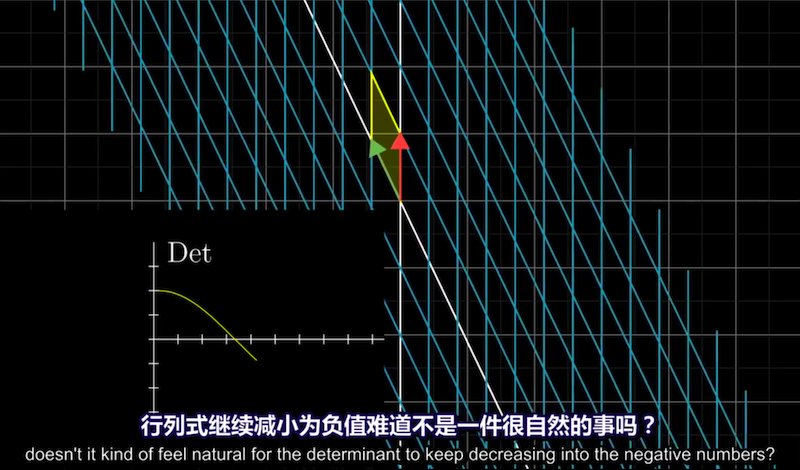
例如$Det(\mathbf{A}) = -5$的几何解释: 变换后空间被翻转,且面积扩大为原来的5倍。
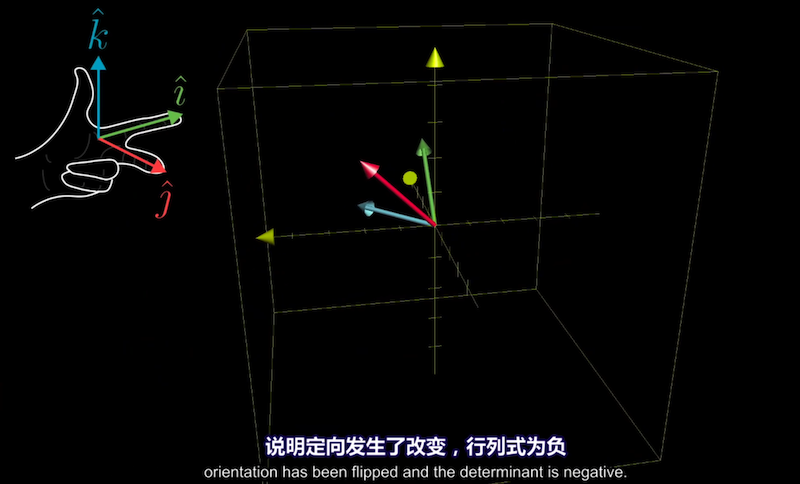
i帽逐渐靠近j帽,面积变为0,然后i帽继续移动,orientation改变,面积变为负。
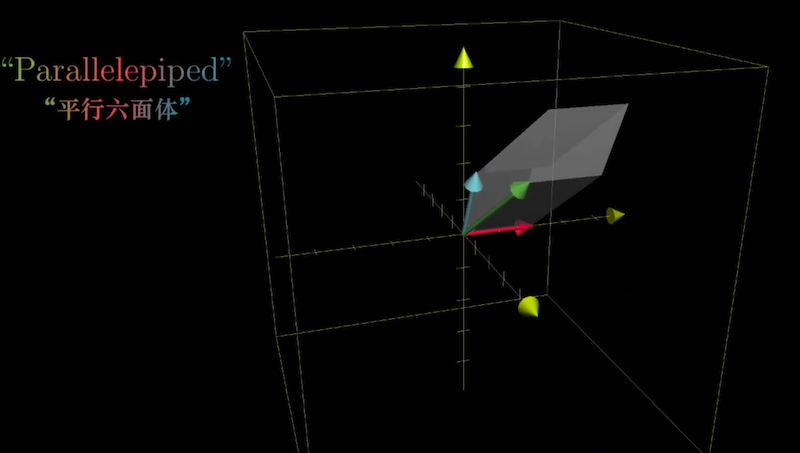
三维行列式的几何直观:Parallelepiped
变换后基向量$L(\hat{i})$ $L(\hat{j})$ $L(\hat{k})$所夹平行六面体的体积 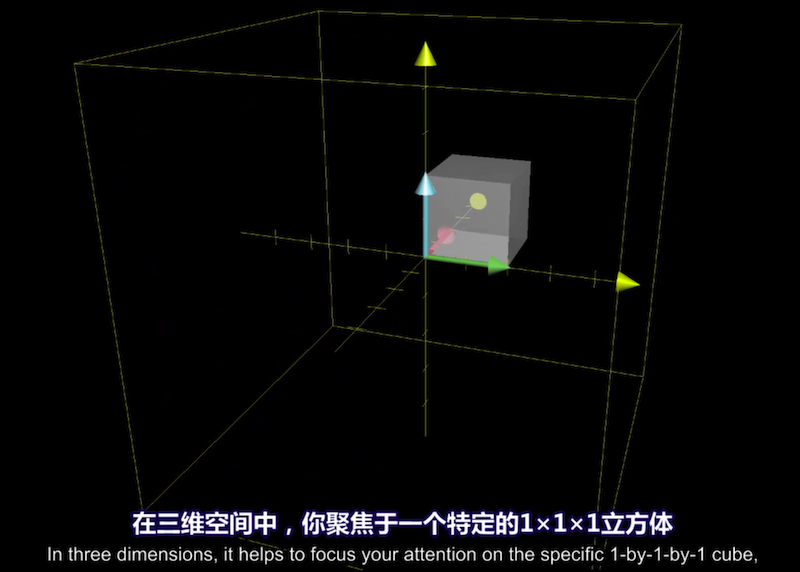
因为立方体的初始体积为1,行列式给出的是体积缩放比例。可以把行列式看作平行六面体的体积。
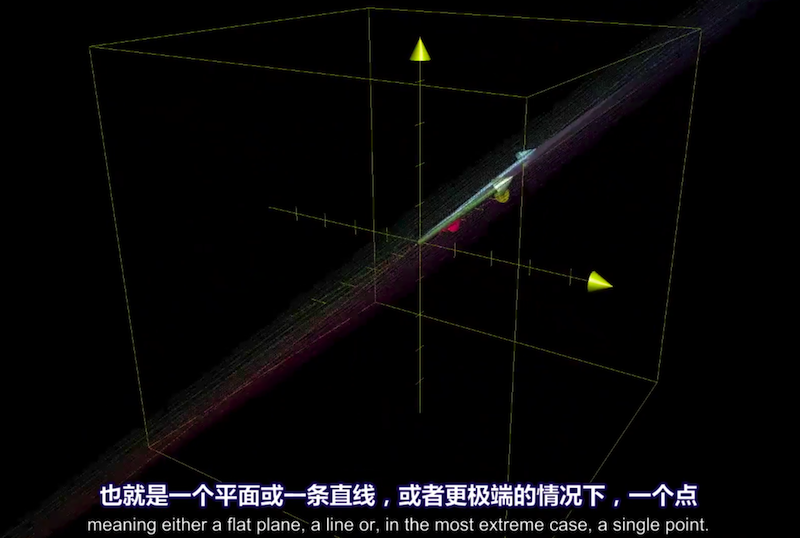
三维行列式为0的几何意义
意味着整个空间被压缩为零体积的东西。
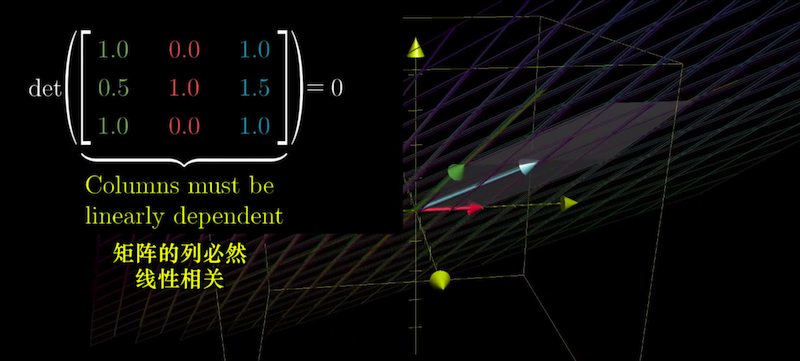
例子:矩阵的列线性相关$L(\hat{k}) = L(\hat{i}) + L(\hat{j})$,行列式为0, 产生降维作用.
D= 0时矩阵的列向量必然线性相关.
三维行列式负值的几何直观
描述三维空间的定向(Orientation): i j k满足右手定则为正,满足左手定则为负。
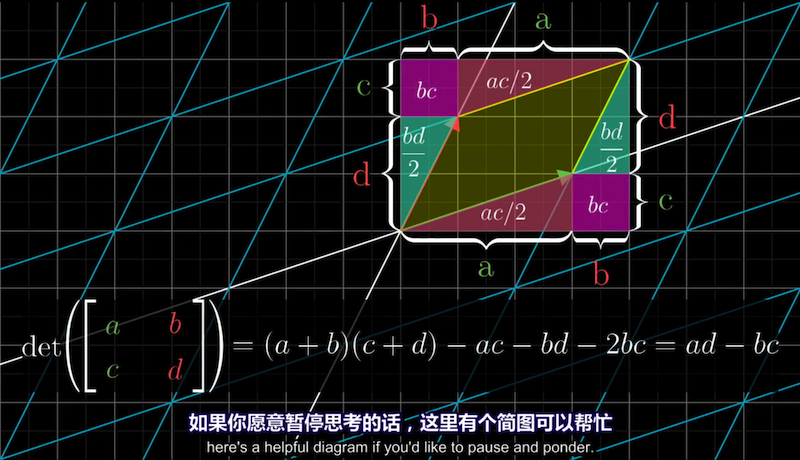
二维行列式计算公式的几何直观
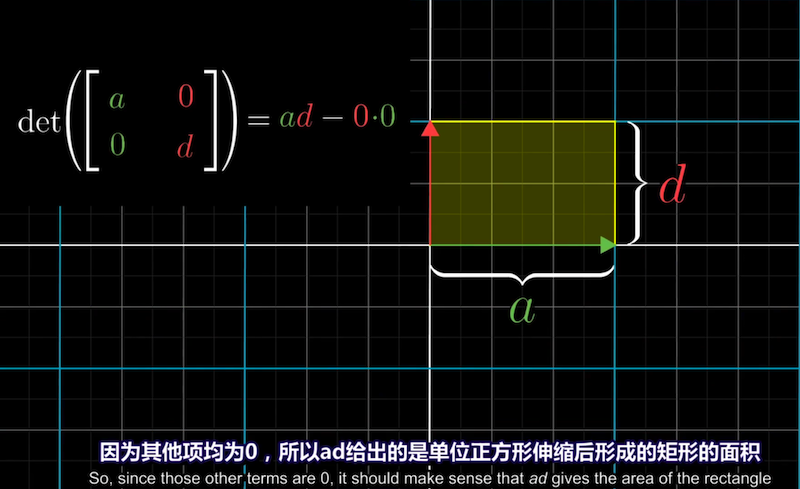
即便b,c其中一个为0
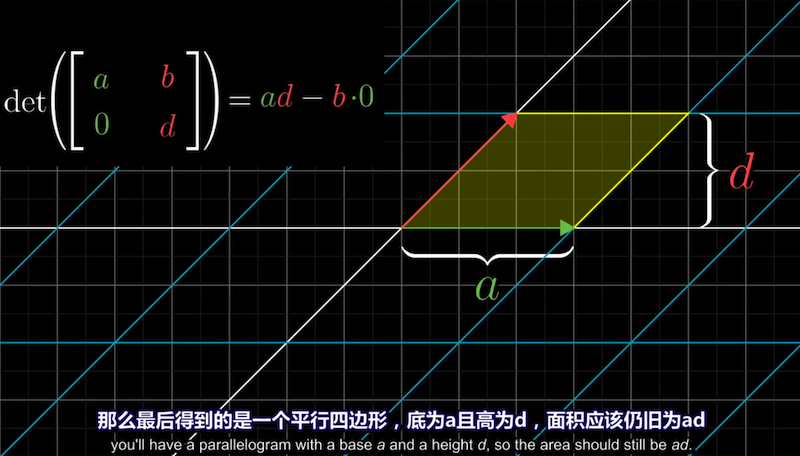
当bc都是不为0的一般情况,bc项实际上表示的是平行四边形在对角方向上压缩了多少。
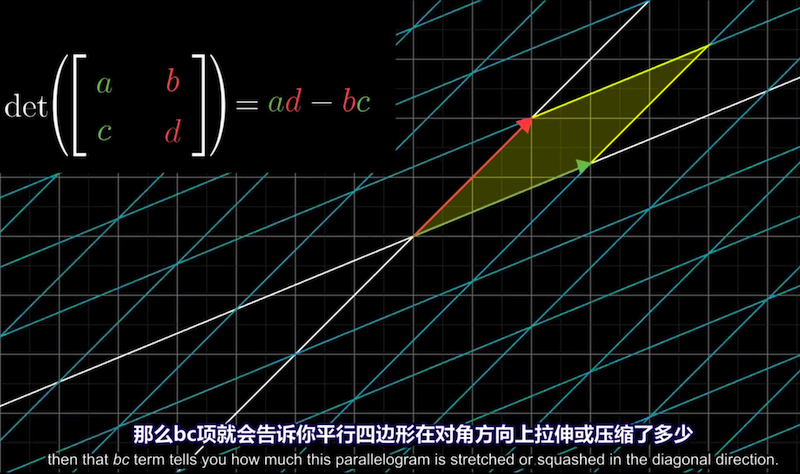
ad - bc的可视化
3阶行列式的计算方法参考其他教材(例如GS的I2AL提到的先消元再算pivot之积、big formula和cofactor)

证明$|M_1M_2 | = | M_1 | | M_2 |$用数值计算比较麻烦,
用行列式的几何意义来看则是trivial的结论。

行列式是线性变换对空间的缩放系数。
