P2 向量究竟是什么？

物理观点：向量是空间中的箭头，只要长度和方向不变，自由移动后仍是同一个向量。
CS观点：vector <=> list of numbers 向量就是有序的数字列表, 例如用向量对房屋建模，
需要房屋面积和价格两个feature。
数学家试图推广这两种观点，只要保证两向量相加和数字与向量数乘有意义即可。
线代中的向量通常以原点为起点，向量的坐标是一组数，指导你如何从起点到达终点 (尖端)

​

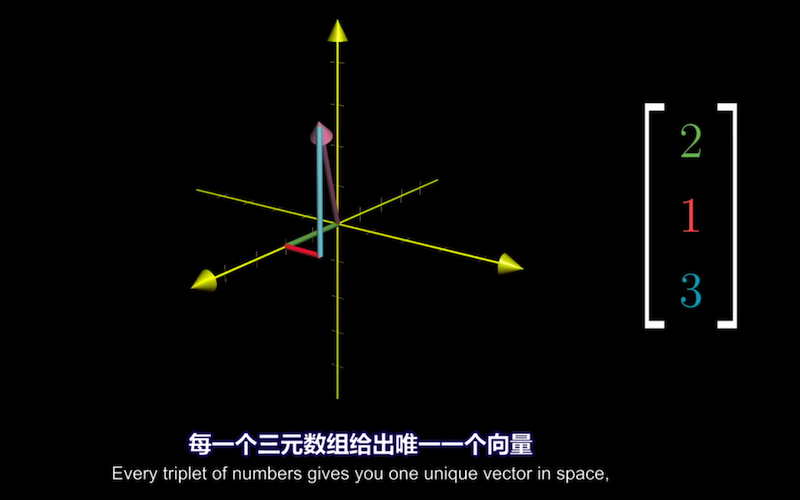
线性代数围绕着两种基本运算：向量相加和向量数乘。
线性代数为大量数据列表提供了概念化、可视化的渠道，使数据的pattern变得更清晰，
也给物理学家和计算机图形学程序员提供了描述和操纵空间的语言。

P3 线性组合、张成的空间与基 Linear combinations, span and bases

把每个向量的坐标(x,y)看成scalar作用于xy坐标系的基向量$\hat{\mathbf{i}}$, $\hat{\mathbf{j}}$， 这个向量
实际上就是两个缩放后的基向量之和 $x\hat{\mathbf{i}}+y\hat{\mathbf{j}}$
基向量用于构建坐标系。如果换一对基向量(不是标准的单位向量), 得到这
同一向量所需的scalar完全不同，从而意识到一个事实：
我们描述向量所用的坐标数字，都依赖于所使用的基。

任意两个不共线的非零向量，所张成的空间是整个二维平面。
(平面上画两条不平行的相交直线，由平行四边形法则，可以到达平面上任意一点)
如果共线，张成的空间就是一条直线；如果都是零向量，只能固定在原点。
因此换一对不共线的新的基向量，仍然能得到任意一个二维向量，

同样允许我们在坐标数字和二维向量之间自由转化。
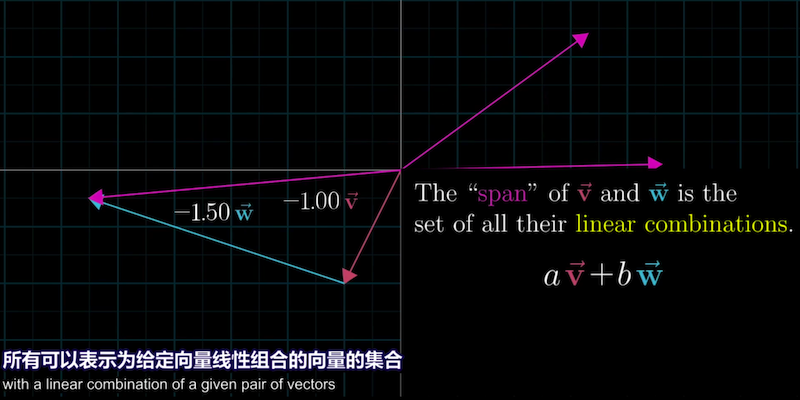
两个向量张成的空间(span)实际上是在问：仅通过向量加法和向量数乘两种基本运算，
能得到的所有可能向量的集合是什么？

​

线性相关： 为了描述一组向量中至少有一个是多余的(二维向量共线，3个三维向量共面等情况)
没有对张成空间的增大做出任何贡献，移除其中一个不会减小张成空间。
多余的向量可以表示为其他向量的线性组合，因为多余的向量就落在已张成的空间中。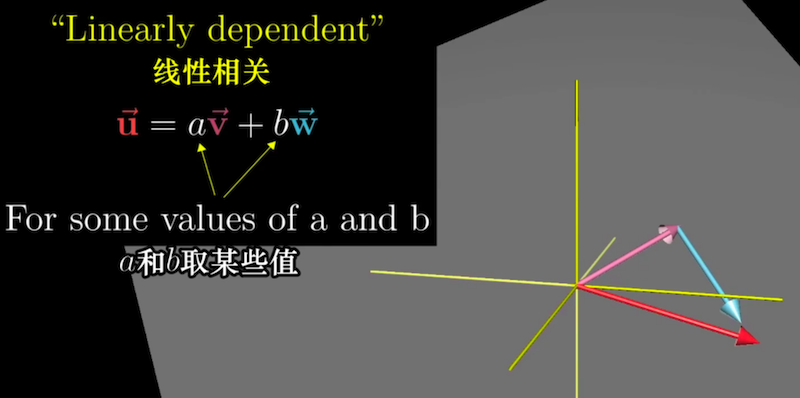

相反地，如果每个向量都给张成空间增添了新的维度，则称为线性无关

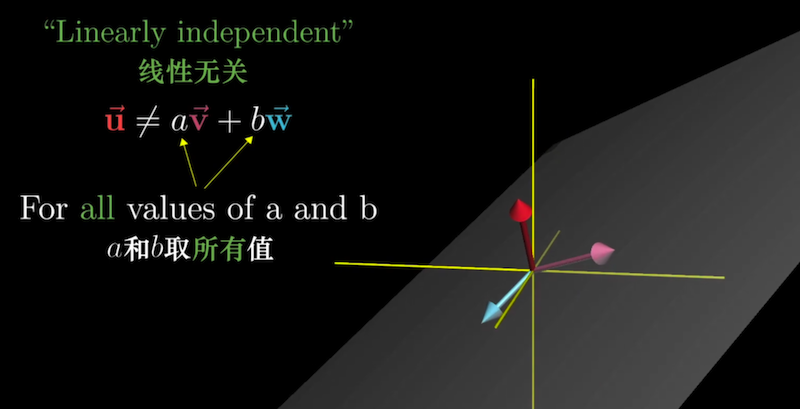
基的严格定义：向量空间的一组基是张成该空间的一个线性无关向量集。

P4 矩阵与线性变换 Linear transformation

变换transformation实际上是function，可理解为向量的函数。

何谓线性变换: 一是直线在变换后仍为直线，不能有所弯曲；二是原点不能移动。
线性变换就是保持原点不动、保持网格线平行且等距的变换。
保持直线但原点移动是仿射变换 (Affine Transformation)

“网格线不等距”的变换举例：对角线被弯曲了

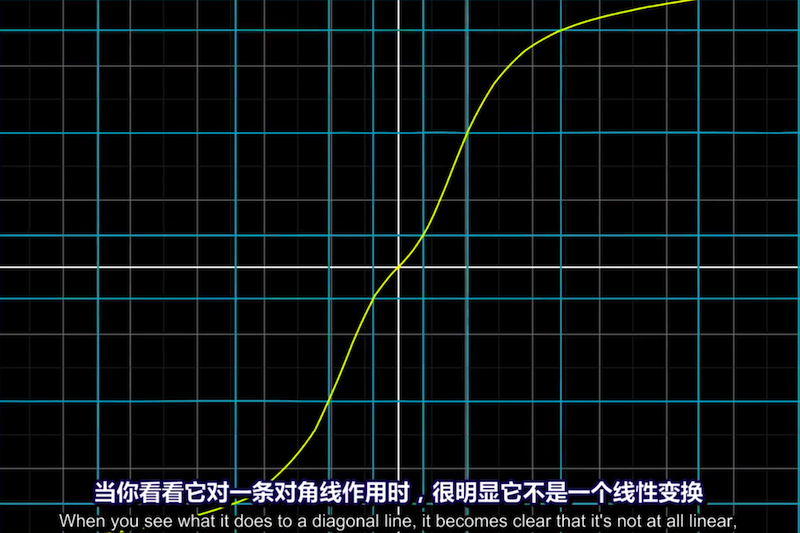
线性变换应看成“保持网格线平行且等距分布“ 的变换 （keeping grid lines parallel and evenly spaced)

问题：如何用数值来描述线性变换？

使得输入一个向量的坐标，输出一个线性变换后的向量坐标。
由上节知识，输入向量可看成是单位基向量一个线性组合(以xy放缩再相加)，
又因为线性变换保持网格线平行且等距，经过变换后的向量，即输出向量和
变换后的基向量也满足相同的关系（与变换前的线性组合，即输入向量的坐标相同)

​

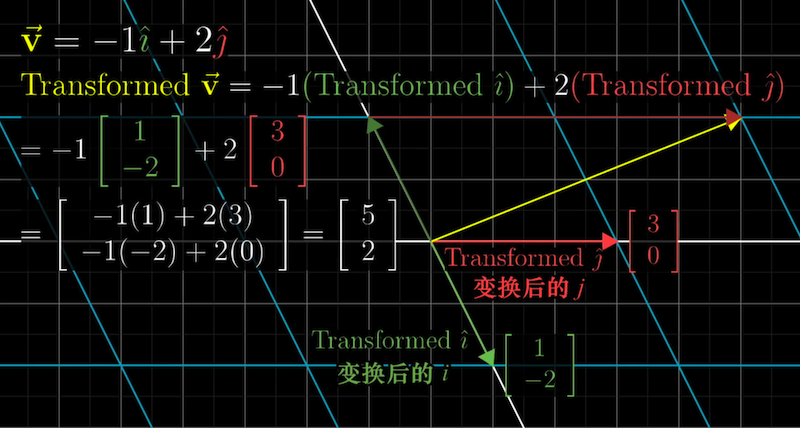
只要记录了变换后的基向量i帽和j帽，就能推出任意向量变换后的位置，而不必去具体研究变换本身。
因此，一个二维线性变换仅用四个数字（变换后基向量的坐标）就可以完全描述。
矩阵实际上就是变换后的基向量列表，打包了描述线性变换的信息。

矩阵左乘输入向量可以看成列向量的线性组合 (以输入向量的坐标为scalar)
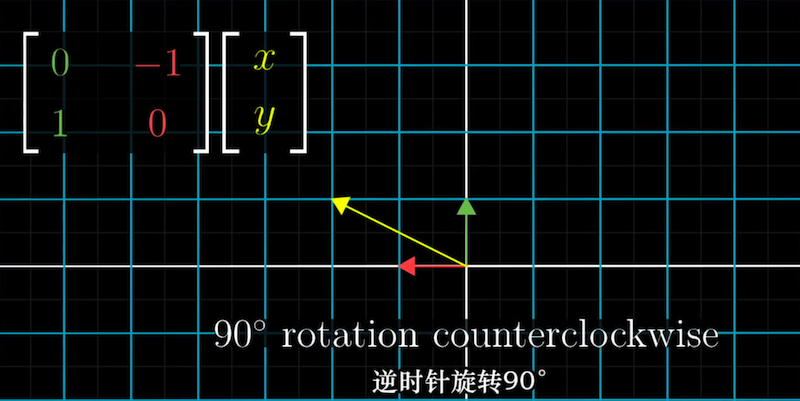
矩阵描述线性变换的实例1：逆时针旋转90度

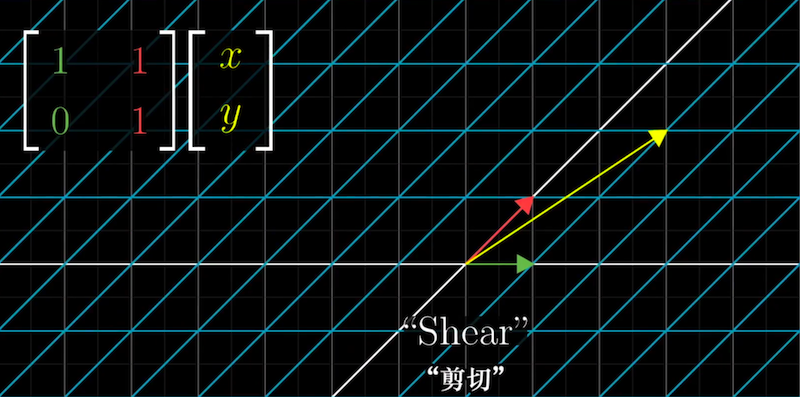
实例2：shear

从矩阵提供的信息出发，想象线性变换的过程。
例子：变换后的基向量线性相关，则这个线性变换把整个二维空间挤压到一条直线上。
\

​
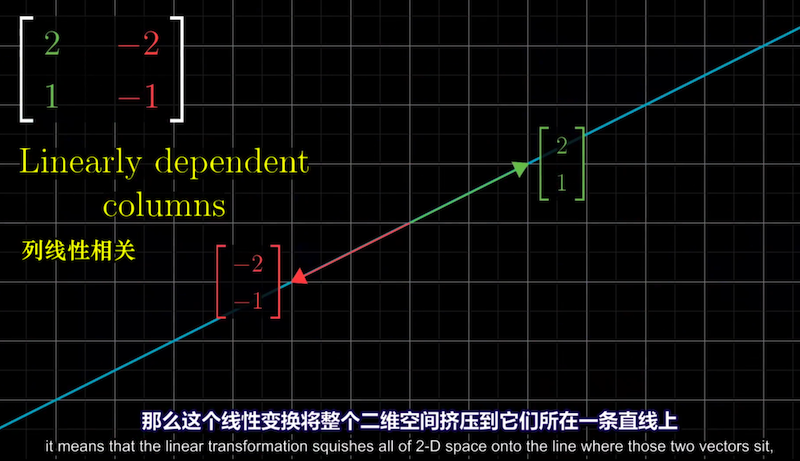总结：线性变换就是以一种“保持网格线平行且等距”的方式扭曲空间，
变换后基向量构成的矩阵，提供了一种描述线性变换的语言，
矩阵左乘向量就像函数f(x)一样，输出变换后的向量坐标。
以后每当你看到一个矩阵，都可以把它解释成一种对空间的特定变换。