三角函数诱导公式:奇变偶不变,符号看象限
三角函数诱导公式的一般形式是:
\(\begin{align*} \hspace{8em} \sin / \cos / \tan / \cot \left(\dfrac{k\pi}{2}\pm\alpha\right) &=\ ?,\ k \in Z \\ \end{align*}\)
- “奇变偶不变”说的是如果参数 $k$ 是奇数($\dfrac{\pi}{2}$的奇数倍),则正弦变余弦 $(\sin \rightarrow \cos)$,
余弦变正弦 $(\cos \rightarrow \sin)$,正切变余切 $(\tan \rightarrow \cot)$,余切变正切 $(\cot \rightarrow \tan)$,即
函数名变为原来的余函数。如果参数 $k$ 是偶数,则保持原式的函数名不变。 - 符号看象限指的是假设 $\alpha$ 为锐角,根据 $\dfrac{k\pi}{2}\pm\alpha$ 所在象限判断原式的符号,若原式 为负则最终式子前面要加符号;若原式为正则最终式子也为正。
三角函数符号象限图如下。记忆口诀:一全正,二正弦,三正切,四余弦。
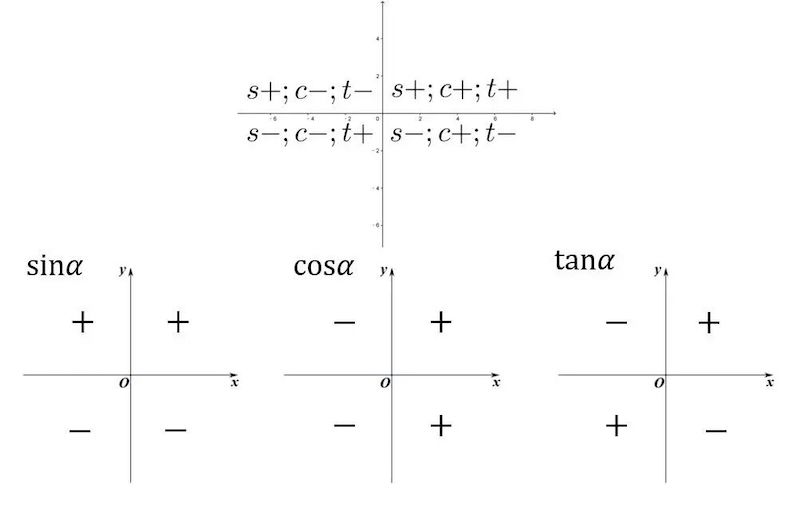
现在我们可以化简任意一个三角诱导公式,例如: $ \sin(\dfrac{3\pi}{2}-\alpha) = \ ?$
这里 $k = 3$ 是 $\dfrac{\pi}{2}$ 的奇数倍,所以函数名要变为 $\cos$ , 然后把 $\alpha$ 看成锐角,则
$\dfrac{3\pi}{2}-\alpha$ 的终边落在第三象限,原式$\sin$ 值为负,所以$\cos$ 前面加符号得$-\cos{\alpha}$。
其他例子比如 $\cos(\pi-\alpha) = -\cos\alpha$, $\sin(\pi-\alpha)=\sin\alpha$
差角公式
\[\begin{align} \cos(\alpha-\beta)=\cos\alpha \cos\beta +\sin\alpha\sin\beta \tag{1} \label{差角余弦}\\ \sin(\alpha-\beta) = \sin\alpha\cos\beta - \cos\alpha\sin\beta \tag{2} \label{差角正弦}\\ \tan(\alpha-\beta) = \dfrac{\tan\alpha-\tan\beta}{1+\tan\alpha\tan\beta} \tag{3}\label{差角正切} \end{align}\]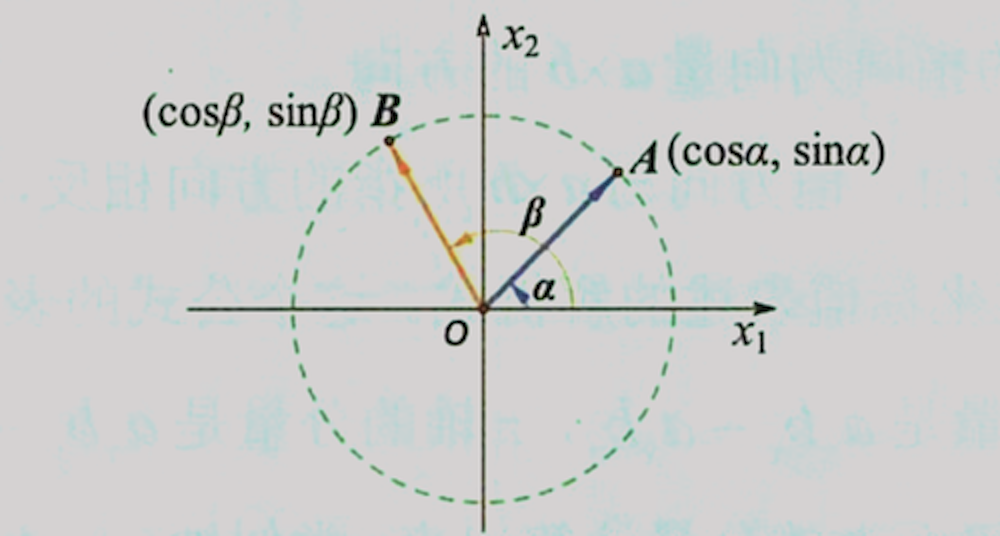
Proof. 可用向量点积的定义证明公式(1),二维向量叉积定义证明公式(2),(1)/(2)推出公式(3)。
如图,取单位圆上的半径向量$\overrightarrow{OA}=(\cos\alpha,\cos\alpha)$,$\overrightarrow{OB}=(\cos\beta,\sin\beta)$
由点积的定义,
\(\overrightarrow{OA} \cdot \overrightarrow{OB} = |\overrightarrow{OA}| |\overrightarrow{OB}|\cos(\beta-\alpha) = \cos\alpha\cos\beta +\sin\alpha\sin\beta\)
$\because |\overrightarrow{OA}|=|\overrightarrow{OB}|=1$ , $\,\cos(\beta-\alpha)=\cos(\alpha-\beta)$
$\therefore \cos(\alpha-\beta)=\cos\alpha\cos\beta +\sin\alpha\sin\beta \qquad$ 公式(1)得证
由二维向量叉积的行列式定义,
\(\begin{align} \overrightarrow{OA} \times \overrightarrow{OB} &= |\overrightarrow{OA}| |\overrightarrow{OB}|\sin(\beta-\alpha) = \begin{vmatrix} \cos\alpha & \sin\alpha \\ \cos\beta & \sin\beta\end{vmatrix}\\ & = \cos\alpha\sin\beta -\sin\alpha\cos\beta \end{align}\)
$\because |\overrightarrow{OA}|=|\overrightarrow{OB}|=1$,
$\therefore \sin(\alpha-\beta)=-\sin(\beta-\alpha)= \sin\alpha\cos\beta -\cos\alpha\sin\beta \qquad$公式(2)得证
\(\begin{align}\tan(\alpha-\beta)&=\dfrac{\sin(\alpha-\beta)}{\cos(\alpha-\beta)} \\ &= \dfrac{\sin\alpha\cos\beta-\cos\alpha\sin\beta}{\underline{\cos\alpha\cos\beta}+\sin\alpha\sin\beta} = \dfrac{\frac{\sin\alpha\cos\beta}{\cos\alpha\cos\beta}-\frac{\cos\alpha\sin\beta}{\cos\alpha\cos\beta}}{1+\frac{\sin\alpha\sin\beta}{\cos\alpha\cos\beta}} \\ &= \dfrac{\tan\alpha-tan\beta}{1+tan\alpha\tan\beta} \qquad \text{公式(3)得证} \end{align}\)
和角公式
\[\begin{align} \cos(\alpha+\beta)=\cos\alpha \cos\beta -\sin\alpha\sin\beta \tag{4} \\ \sin(\alpha+\beta) = \sin\alpha\cos\beta + \cos\alpha\sin\beta \tag{5} \\ \tan(\alpha+ \beta) = \dfrac{\tan\alpha+\tan\beta}{1-\tan\alpha\tan\beta} \tag{6} \end{align}\]Proof. 把差角公式(1)(2)(3)中的$\beta$ 替换为$-\beta$ 即可得到和角公式(4)(5)(6)
倍角公式
\[\begin{align} \cos2\alpha &=\cos^2\alpha -\sin^2\alpha = 1-2\sin^2\alpha= 2\cos^2\alpha-1 \tag{7} \\ \sin2\alpha &= 2\sin\alpha\cos\alpha \tag{8} \\ \tan2\alpha &= \dfrac{2\tan\alpha}{1-\tan^2\alpha} \tag{9} \end{align}\]Proof. 在和角公式(4)(5)(6)中令$\beta = \alpha $ 即可得到倍角公式(7)(8)(9)
半角公式
\[\begin{align} \sin\frac{\theta}{2}&= \pm\sqrt{\dfrac{1-\cos\theta}{2}} \tag{10} \\ \cos\frac{\theta}{2}&=\pm\sqrt{\dfrac{1+\cos\theta}{2}} \tag{11}\\ \tan\frac{\theta}{2}&=\pm\sqrt{\dfrac{1-\cos\theta}{1+\cos\theta}}=\dfrac{\sin\theta}{1+\cos\theta}=\dfrac{1-\cos\theta}{\sin\theta} \tag{12} \end{align}\]Proof. 把$\alpha=\dfrac{\theta}{2}$ 代入二倍角公式(7) $\cos2\alpha = 1-2\sin^2\alpha $ 得
$\cos\theta=1-2\sin^2\dfrac{\theta}{2},\quad \sin^2\dfrac{\theta}{2}=\dfrac{1-\cos\theta}{2},\quad $
$\sin\dfrac{\theta}{2}=\pm\sqrt{\dfrac{1-\cos\theta}{2}}\quad$ 公式(10)得证。
把 $\alpha=\dfrac{\theta}{2}$代入二倍角公式(7) $\cos2\alpha=2\cos^2\alpha -1$ 得
$\cos\theta = 2\cos^2\dfrac{\theta}{2}-1,\quad$$\cos^2\dfrac{\theta}{2}=\dfrac{1+\cos\theta}{2},$
$\cos\dfrac{\theta}{2}=\pm\sqrt{\dfrac{1+\cos\theta}{2}}\quad$公式(11)得证。 \(\begin{align} \tan\dfrac{\theta}{2}=\dfrac{\sin\frac{\theta}{2}}{\cos\frac{\theta}{2}}&=\pm\sqrt{\dfrac{1-\cos\theta}{1+\cos\theta}} \\ &=\pm\sqrt{\dfrac{(1-\cos\theta)(1+\cos\theta)}{(1+\cos\theta)(1+\cos\theta)}}=\pm\sqrt{\dfrac{1-\cos^2\theta}{(1+\cos\theta)^2}} =\pm\sqrt{\dfrac{\sin^2\theta}{(1+\cos\theta)^2}}\\ &=\pm\sqrt{\dfrac{(1-\cos\theta)(1-\cos\theta)}{(1+\cos\theta)(1-\cos\theta)}}=\pm\sqrt{\dfrac{(1-\cos\theta)^2}{1-\cos^2\theta}} =\pm\sqrt{\dfrac{(1-\cos\theta)^2}{\sin^2\theta}} \end{align}\) $\tan\dfrac{\theta}{2}\,\sin\theta=\dfrac{\sin\frac{\theta}{2}}{\cos\frac{\theta}{2}}\cdot 2\sin\dfrac{\theta}{2}\cos\dfrac{\theta}{2}=2\sin^2\dfrac{\theta}{2} \ge 0$
当 $2\sin^2\dfrac{\theta}{2} = 0,$ 即 $\sin\dfrac{\theta}{2}=0$,则此时 $\tan\dfrac{\theta}{2}$ 和 $\sin\theta$ 都为0
$\therefore \tan\dfrac{\theta}{2}$和 $\sin\theta $ 总是同号
又$\because 1\pm\cos\theta $ 总是非负,所以等式右边的$\pm$号是多余的。
$\therefore \tan\dfrac{\theta}{2} = \dfrac{\sin\theta}{1+\cos\theta}=\dfrac{1-\cos\theta}{\sin\theta}\quad$ 公式(12)得证。
积化和差公式
\[\begin{align} \sin\alpha\cos\beta = \dfrac{\sin(\alpha+\beta)+\sin(\alpha-\beta)}{2} \tag{13}\\ \cos\alpha\sin\beta=\dfrac{\sin(\alpha+\beta)-\sin(\alpha-\beta)}{2} \tag{14}\\ \cos\alpha\cos\beta=\dfrac{\cos(\alpha+\beta)+\cos(\alpha-\beta)}{2} \tag{15}\\ \sin\alpha\sin\beta=-\dfrac{\cos(\alpha+\beta)-\cos(\alpha-\beta)}{2} \tag{16} \end{align}\]Proof. 由和角公式(5)与差角公式(2),$\sin(\alpha+\beta)=\sin\alpha\cos\beta+\cos\alpha\sin\beta,\quad \sin(\alpha-\beta)=\sin\alpha\cos\beta-\cos\alpha\sin\beta$
$(5)+(2)$ 得 $\sin(\alpha+\beta)+\sin(\alpha-\beta)=2\sin\alpha\cos\beta$
$(5)-(2)$ 得 $\sin(\alpha+\beta)-\sin(\alpha-\beta)=2\cos\alpha\sin\beta$
等式两边同除以2即得到公式(13)和(14)
由和角公式(4)与差角公式(1),$\cos(\alpha+\beta)=\cos\alpha\cos\beta-\sin\alpha\sin\beta,\quad\cos(\alpha-\beta)=cos\alpha\cos\beta+\sin\alpha\sin\beta$
$(4)+(1)$ 得 $\cos(\alpha+\beta)+\cos(\alpha-\beta)=2\cos\alpha\cos\beta$
$(4)-(1)$ 得 $\cos(\alpha+\beta)-\cos(\alpha-\beta)=-2\sin\alpha\sin\beta$
分别两边除以2和-2即得到公式(15)和(16)
和差化积公式
\[\begin{align} \sin A+\sin B=2\sin\dfrac{A+B}{2}\cos\dfrac{A-B}{2} \tag{17} \\ \sin A-\sin B=2\cos\dfrac{A+B}{2}\sin\dfrac{A-B}{2} \tag{18} \\ \cos A+\cos B=2\cos\dfrac{A+B}{2}\cos\dfrac{A-B}{2} \tag{19} \\ \cos A-\cos B=-2\sin\dfrac{A+B}{2}\sin\dfrac{A-B}{2} \tag{20} \end{align}\]Proof. 令 $\alpha+\beta = A, \alpha-\beta=B,$ 则 $\alpha=\dfrac{A+B}{2},\beta=\dfrac{A-B}{2}$
代入(13)(14)可得公式(17)(18),代入(15)(16)可得公式(19)(20)
